Riassunto di Analisi II — Appunti TiTilda

Questa pagina è la seconda versione, per la prima versione, visitare questa pagina.

Capitolo Uno: Equazioni differenziali

1.1 Equazioni differenziali ordinarie (EDO)

Risolvere un’equazione differenziale vuol dire trovare una funzione $y(t)$ che soddisfa un’equazione del tipo $y'(t) = f(t, y(t))$ (un equazione del genere è detta in forma normale).

Si dice integrale generale l’insieme di tutte le soluzioni di una EDO.

Una EDO si dice del primo ordine se contiene al massimo occorrnze della derivata prima della funzione incognita.

Per trovare il dominio di una EDO, si scrive $f(t, s)$ e si trovano le condizioni di esistenza sul piano t-s.

1.2 Soluzioni costanti

Una soluzione costante è una soluzione della forma $y(t) = k \quad \forall t$. Per trovare le soluzioni costanti, so sostituisce nella EDO $y(t)$ con $k$ e $y'(t)$ con $0$ (infatti la derivata di una costante è nulla) e si risolve per $k$ l’equazione ottenuta.

1.3 EDO a variabili separabili

Una EDO del primo ordine si dice a variabili separabili se è della forma $y'(t) = h(t) \cdot g(y(t))$ con $h : J_1 \sube \mathbb{R} \to \mathbb{R}$ e $g : J_2 \sube \mathbb{R} \to \mathbb{R}$ continue.

Si dice a variabili separabili perchè è possibile portare da un lato tutte le occorrenze di $y(t)$ e $y'(t)$ lasciando dall’altro tutte le occorrenze di $t$.

Le soluzioni costanti di una EDO a variabili separabili sono $y(t) = c$ dove $c$ sono le soluzioni di $g(c) = 0$.

Per risolvere una EDO a variabili separabili, è necessario seguire una procedura predefinita:

1. Da $y'(t) = h(t) \cdot g(y(t))$ trovo che $f(t, y(t)) = h(t) \cdot g(y(t))$ quindi $f(t, s) = h(t) \cdot g(s)$.
2. Trovo le soluzioni costanti $y(t) = s$ imponendo $g(s) = 0$.
3. Divido l’equazione originale da entrambi i lati per $g(y(t))$ e integro da entrambi i lati da $t_0$ a $t$, ottenendo $$\int_{t_0}^t \frac{y'(t)}{g(y(t))} dt = \int_{t_0}^t h(t) dt$$ Il lato destro viene risolto normalmente, il lato sinistro diventa $$\int_{t_0}^t \frac{y'(t)}{g(y(t))} dt = \int_{y(t_0)}^{y(t)} \frac{1}{g(y)} dy$$ e si risolve per $t(t)$, inglobando tutte le costanti in $C$ (o altre lettere se la $C$ è già stata utilizzata).

1.4 Problema di Cauchy per una EDO del primo ordine

Data una EDO del primo ordine $y'(t) = f(t, y(t))$, sia $(t_0, y_0)$ un punto appartenente al dominio di $f$. Il problema di Cauchy consiste nel determinare una soluzione dell’equazione che passi per quel punto.

$$\begin{cases} y'(t) = f(t, y(t)) \\ y(t_0) = y_0 \end{cases}$$

Per una EDO del primo ordine, viene imposta quindi una sola condizione aggiuntiva.

Per risolvere un problema di Cauchy di tale genere, si seguono i seguenti passaggi:

1. Trovo l’integrale generale.
2. Impongo la condizione aggiuntiva per trovare la $C$.
3. Sostituisco la $C$ nella soluzione originale.

Se il dominio di $f$ è diviso in più parti, è sufficiente considerare solo la regione in cui si trova il punto $(t_0, y_0)$.

1.5 EDO del primo ordine lineari

Una EDO del primo ordine lineare in forma normale è una EDO della forma $y'(t) = a(t) \cdot y(t) + b(t)$ con $a,b : J \sub \mathbb{R} \to R$ continue su $J$.

Teorema di esistenza e unicità globale per il problema di Cauchy

Siano $J \sub \mathbb{R}$, $a,b : J \to \mathbb{R}$ continue su $J$. Per ogni $t_0 \in J$ e $y_0 \in \mathbb{R}$ il problema di Cauchy ha un’unica soluzione definita $\forall t \in J$.

Da questo ne derivano 3 cose molto importanti:

1. Dato un qualunque $(t_0, y_0) \in J \times \mathbb{R}$, c’è una soluzione della EDO che passa per tale punto; i grafici delle soluzioni riempiono tutto $J \times \mathbb{R}$.
2. La soluzione è unica: i grafici non si intersecano.
3. Tutte le soluziono sono definite $\forall t \in J$.

Per risolvere una EDO del primo ordine lineare della forma $y'(t) = a(t) \cdot y(t) + b(t)$, considero $A(t)$ primitiva di $a(t)$, successivamente, moltiplico da entrambi i lati per $e^{-A(t)}$ e porto a sinistra tutti i termini che contengono y:

$$y'(t) \cdot e^{-A(t)} = a(t) \cdot e^{-A(t)} \cdot y(t) + b(t) \cdot e^{-A(t)} \\ y'(t) \cdot e^{-A(t)} - a(t) \cdot e^{-A(t)} \cdot y(t) = b(t) \cdot e^{-A(t)} \\$$

Ora riconosco che $(y(t) \cdot e^{-A(t)})' = y'(t) \cdot e^{-A(t)} - y(t) \cdot e^{-A(t)} \cdot a(t)$ dunque posso sostituire la parte a sinistra dell’uguale con $(y(t) \cdot e^{-A(t)})'$:

$$(y(t) \cdot e^{-A(t)})' = b(t) \cdot e^{-A(t)}$$

Per il teorema fondamentale del calcolo integrale, posso integrare da ambo i lati, poi isolo $y(t)$:

$$\int_{t_0}^t \left(y(x) \cdot e^{-A(x)} \right)' dx = \int_{t_0}^t b(x) \cdot e^{-A(x)} dx \\ \left[ y(x) \cdot e^{-A(x)} \right]_{t_0}^{t} = \int_{t_0}^t b(x) \cdot e^{-A(x)} dx \\ y(t) \cdot e^{-A(t)} - \underbrace{y(t_0) \cdot e^{-A(t_0)}}_{= C} = \int_{t_0}^t b(x) \cdot e^{-A(x)} dx \\ y(t) \cdot e^{-A(t)} = \int_{t_0}^t b(x) \cdot e^{-A(x)} dx + C \\ y(t) = e^{A(t)} \left( \int_{t_0}^t b(x) \cdot e^{-A(x)} dx + C \right)$$

E’ detta omogenea una EDO lineare con $b(t) = 0 \forall t$.

In tal caso, l’EDO è anche a variabili separabili e si può risolvere come si preferisce.

1.6 Equazioni di Bernoulli

Un’equazione di Bernoulli è una EDO del primo ordine non lineare della forma $y'(t) = k(t) \cdot y(t) + h(t) \cdot y(t)^\alpha$ con $\alpha \in \mathbb{R}$, $\alpha \ne 0$, $\alpha \ne 1$, $h, k$ continue.

Se $\alpha$ è irrazionale oppure è razionale con denominatore pari, allora $y^\alpha$ ha senso solo se $y \ge 0$. Per semplificare, verrà trattato solo il caso di $y \gt 0 \quad \forall \alpha$. Per $\alpha \in \{0, 1\}$, non vale il teorema di unicità. Se $\alpha \lt 0$ non ha senso $y = 0$.

Per risolvere un’equazione di Bernoulli, c’è un procedimento da seguire.

Inizio cercando le soluzioni costanti:

• $y(t) = 0$ è sempre soluzione.
• Se sia $h$ che $k$ sono costanti, posso raccogliere $y(t)$e trovare un’altra soluzione costante: $$k \cdot y(t) + h \cdot y(t)^\alpha = 0 \\ y(t) \cdot (k + h \cdot y(t)^{\alpha - 1}) = 0 \\ k + h \cdot y(t)^{\alpha - 1} = 0 \\ y(t)^{\alpha - 1} = -\frac{k}{h} \\ y(t) = \left( -\frac{k}{h} \right)^{\frac{1}{\alpha - 1}}$$

Procedo cercando le soluzioni non costanti dividendo da entrambi i lati per $y(t)^\alpha$:

$$\frac{y'(t)}{y(t)^\alpha} = k(t) \cdot y(t)^{1 - \alpha} + h(t)$$

Pongo $z(t) = y(t)^{1 - \alpha}$ e calcolo $z'(t)$:

$$\begin{align*} z'(t) &= (1 - \alpha) \cdot y(t)^{1 - \alpha - 1} \cdot y'(t)\\ &= (1 - \alpha) \cdot \frac{y'(t)}{y(t)^\alpha} \\ &= (1 - \alpha) \cdot \left( k(t) \cdot y(t)^{1 - \alpha} + h(t) \right) \\ &= (1 - \alpha) \cdot \left( k(t) \cdot z(t) + h(t) \right) \\ &= \underbrace{(1 - \alpha) \cdot k(t)}_{a(t)} \cdot z(t) + \underbrace{(1 - \alpha) \cdot h(t)}_{b(t)} &= a(t) \cdot z(t) + b(t) \end{align*}$$

Ora che ho ottenuto un’equazione lineare, la risolvo per $z(t)$ e poi ritorno in $y$:

$$y(t) = z(t)^\frac{1}{1 - \alpha}$$

1.7 EDO del secondo ordine lineari

Una EDO del secondo ordine lineare è un’equazione della forma $a(t) \cdot y''(t) + b(t) \cdot y'(t) + c(t) \cdot y(t) = f(t)$ con $a, b, c, f : J \sube \mathbb{R} \to \mathbb{R}$ e $a \ne 0$.

1.8 Problema di Cauchy per una EDO del secondo ordine lineare

Il problema di Cauchy per una EDO del secondo ordine è analogo al problema di Cauchy per una EDO del primo ordine, ma vengono imposte, al posto che una, due condizioni aggiuntive che vanno a vincolare sia la $y$ che la $y'$. In particolare, un problema di Cauchy per una EDO lineare del secondo ordine è un sistema della forma

$$\begin{cases} a(t) \cdot y''(t) + b(t) \cdot y'(t) + c(t) \cdot y(t) = f(t) \\ y(t_0) = y_0 \\ y'(t_0) = v_0 \end{cases}$$

Teorema di esistenza e unicità globale per il problema di Cauchy

Data la EDO $a(t) \cdot y''(t) + b(t) \cdot y'(t) + c(t) \cdot y(t) = f(t)$ con $a, b, c, f, : J \sube \mathbb{R} \to \mathbb{R}$ continue e $a \ne 0$ in $J$ e assegnati $t_0 \in J$ e $y_0, v_0 \in \mathbb{R}$ allora il problema di Cauchy definito come sopra ha un’unica soluzione $y(t)$ definita $\forall t \in J$.

Per il principio di sovrapposizione, se $y_1$ e $y_2$ sono soluzione della stessa EDO, $y_1 - y_2$ è soluzione della EDO omogenea associata e tutte le soluzioni di quest ultima formano uno spazio vettoriale

Teorema di struttura dell’integrale generale di EDO del secondo ordine lineari omogenee

Siano $a,b,c : J \sube \mathbb{R} \to \mathbb{R}$ continue in $J$ con $a \ne 0$.

L’integrale generale dell’equazione omogenea $a(t) \cdot y''(t) + b(t) \cdot y'(t) + c(t) \cdot y(t) = 0$ è uno spazio vettoriale di dimensione 2, cioè le soluzioni sono della forma $y_0(t) = C_1 \cdot y_{o1}(t) + C_2 \cdot y_{o2}(t)$ con $C_1, C_2 \in \mathbb{R}$ dove $y_{o1}$ e $y_{o2}$ sono due soluzioni linearmente indipendenti.

Dimostrazione

Sia $V$ lo spazio vettoriale delle funzioni di classe $\mathcal{C}^2$ su $J$.

L’integrale generale dell’omogenea è il seguente sottoinsieme di $V$:

$$W = \left\{ y \in V : ay'' + by' + cy = 0 \right\} = \ker L$$

dove $L$ è l’operatore definito come $Ly = ay'' + by' + cy$.

In quanto kernel di un’applicazione lineare, $W$ è sottospazio vettoriale.

Per dimostrare che $W$ ha dimensione 2, devo

1. Esibire due soluzioni linearmente indipendenti
2. Dimostrare che ogni altra soluzione si scrive come combinazione lineare delle due soluzioni trovate al punto precedente.

Cerco due soluzioni linearmente indipendenti.

Sia $t_0 \in J$, per il teorema di esistenza e unicità globale, posso scegliere due punti linearmente indipendenti e cercare, per ciascun punto, una soluzione che passa per tale punto.

Scelgo i punti $(1, 0)$ e $(0, 1)$

$$\begin{cases} ay''_{o1} + by'_{o1} + cy_{o1} = 0 \\ y_{o1}(t_0) = 1 \\ y'_{o1}(t_0) = 0 \end{cases} \qquad \begin{cases} ay''_{o2} + by'_{o2} + cy_{o2} = 0 \\ y_{o2}(t_0) = 0 \\ y_{o2}(t_0) = 1 \end{cases}$$

Per verificare che le due soluzioni sono linearmente indipendenti, suppongo, per assurdo, che non lo siano, quindi che $y_{o1}(t) = k \cdot y_{o2}(t) \quad \forall t \in J$.

Per $t = t_0$ si ha che $y_{o1} = k \cdot y_{o2} \iff 1 = k \cdot 0$ che è impossibile, pertanto le due soluzioni sono linearmente indipendenti.

Ora dimostro che qualunque soluzione è combinazione lineare delle due precedenti.

Sia $y_o$ una soluzione qualunque dell’equazione omogenea:

$$y_o(t) = C_1 \cdot y_{o1}(t) + C_2 \cdot y_{o2}(t) \implies \begin{cases} y_o(t_0) = C_1 \cdot y_{o1}(t_0) + C_2 \cdot y_{o2}(t_0) = C_1 \cdot 1 + C_2 \cdot 0 = C_1\\ y'_o(t_0) = C_1 \cdot y'_{o1}(t_0) + C_2 \cdot y'_{o2}(t_0) = C_1 \cdot 0 + C_2 \cdot 1 = C_2 \end{cases}$$

Definisco ora una funzione $z(t) = C_1 \cdot y_{o1}(t) + C_2 \cdot y_{o2}(t) = y_o(t)$. $z(t)$ risolve lo stesso problema di Cauchy di $y_o(t)$ e quindi per il teorema di esistenza e unicità globale del problema di Cauchy, sono la stessa cosa.

1.9 Struttura dell’integrale generale di EDO del secondo ordine lineari non omogenee

Siano $a,b,c : J \sube \mathbb{R} \to \mathbb{R}$ continue in $J$ con $a \ne 0$.

L’integrale generale dell’equazione completa $a(t)y''(t) + b(t)y'(t) + c(t)y(t) = f(t)$ è $y(t) = y_o(t) + y_p(t) = C_1 \cdot y_{o1}(t) + C_2 \cdot y_{o2}(t) + y_p(t)$ con $y_o$ soluzione dell’omogenea associata, $y_{o1}, y_{o2}$ soluzioni particolari linearmente indipendenti dell’omogenea associata e $y_p$ soluzione particolare dell’equazione completa.

In pratica, l’integrale generale di una EDO del secondo ordine lineare non omogenea è uno spazio affine di dimensione due che consiste dello span delle soluzioni dell’omogenea associata, translata di $y_p$.

1.10 Risoluzione di EDO omogenee a coefficienti costanti

Per risolvere una edo omogenea a coefficienti costanti, scrivo il polinomio caratteristico $p(\lambda) = a \lambda^2 + b \lambda + c$ e risolvo l’equazione caratteristica $p(\lambda) = 0$ con $\Delta = b^2 - 4ac$.

A seconda del segno di $\Delta$, l’integrale generale assume forme diverse:

$\Delta$	Integrale Generale
$\Delta \gt 0$	$y(t) = C_1 e^{\lambda_1 t} + C_2 e^{\lambda_2 t}$
$\Delta = 0$	$y(t) = C_1 e^{\lambda t} + C_2 t e^{\lambda t}$
$\Delta \lt 0$	$y(t) = e^{\Re \lambda t}(C_1 \cos(\Im \lambda t) + C_2 \sin(\Im \lambda t))$

La soluzione particolare la si può trovare con il metodo di somiglianza.

1.11 Sistemi differenziali lineari

Un sistema differenziale lineare è un’equazione della forma $\underline y'(t) = A \underline y(t) + \underline b(t)$ con $\underline y', \underline y, \underline b \in (\mathbb{R} \to \mathbb{R})^n$, $A \in \mathcal{M}_\mathbb{R}(n)$.

Tale equazione può essere espansa:

$$\begin{pmatrix} y'_1 \\ \vdots \\ y'_n \end{pmatrix} = A \cdot \begin{pmatrix} y_1 \\ \vdots \\ y_n \end{pmatrix} + \begin{pmatrix} b_1 \\ \vdots \\ b_n \end{pmatrix}$$

Il problema di Cauchy per un sistema differenziale lineare consiste nell’imporre una condizione per ogni $y_i$:

$$\begin{cases} \underline y'(t) = A \underline y(t) + \underline b(t) \\ \underline y(t_0) = \underline y_0 \end{cases}$$

Teorema di esistenza e unicità globale per il problema di Cauchy

Sia $A \in \mathcal{M}_\mathbb{R}(n)$ e $b_i : j \sube \mathbb{R} \to \mathbb{R}$ continue. Dati $t_0 \in J$ e $\underline y_0 \in \mathbb{R}$, il problema di Cauchy enunciato come sopra, ha un’unica soluzione $\underline y(t)$ definita $\forall t$.

Questo teorema ha 2 conseguenze importanti:

1. Se le funzioni $b_i$ sono definite e continue in tutto $\mathbb{R}$ allora le soluzione $y_i(t)$ sono definite in tutto $\mathbb{R}$.
2. Se il sistema è omogeneo ($b_i = 0$) allora $$\begin{cases} \underline y'(t) = A \cdot \underline y(t) \\ \underline y(t_0) = \underline 0 \end{cases}$$ ha una sola soluzione.

Dato un sistema differenziale lineare $n \times n$ omogeneo, chiamiamo sistema fondamentale di soluzioni una famiglia di $n$ soluzioni linearmente indipendenti $\underline y_{o1}(t), \dots, \underline y_{on}(t)$ che costituiscono una base dello spazio vettoriale delle soluzioni del sistema.

1.12 Determinante wronskiano

Supponiamo di conoscere $n$ soluzioni $\underline y_{o1}(t), \dots, \underline y_{on}(t)$ di un sistema differenziale lineare $n \times n$ omogeneo: il sistema fondamentale esiste se e solo se esiste un $t_0$ (tipicamente 0) tale che $\det(\underline y_{o1}(t) | \dots | \underline y_{on}(t)) \ne 0$.

Si chiama matrice wronskiana la matrice ottenuta affiancando un sistema fondamentale:

$$W = \underline y_{o1}(t), \dots, \underline y_{on}(t)$$

Con questa notazione, l’integrale generale del sistema omogeneo diventa $\underline y_o(t) = W(t) \cdot \underline C$ con $\underline C \in \mathbb{R}$ e la soluzione del problema di Cauchy si ottiene scegliendo $\underline C = W(t_0)^{-1} \cdot \underline y_o$ quindi $\underline y(t) = W(t) \cdot [W(t_0)]^{-1} \cdot \underline y_o$.

1.13 Risoluzione esplicita di sistemi con $A$ diagonalizzabile reale

Se $A \in \mathcal{M}_\mathbb{R}(2)$ è diagonalizzabile reale ($A$ è diagonalizzabile reale $\iff$ esistono $n$ autovettori di $A$ che formano una base di $\mathbb{R}^n$ $\iff$ tutti gli autovalori sono regolari; se $A$ è simmetrica o ha $n$ autovalori reali distinti, allora è diagonalizzabile reale), detta $S$ la matrice ottenuta affiancando una base di $\mathbb{R}^n$, vale che

$$S = (\underline v_1 | \dots | \underline v_n) \qquad S^{-1} \cdot A \cdot S = \Lambda \qquad \Lambda = \text{diag}(\lambda_1, \dots, \lambda_s) \qquad A = S \cdot \Lambda \cdot S^{-1}$$

Una matrice wronskiana relativa al sistema omogeneo è $W(t) = (e^{\lambda_1 t} \underline v_1| \dots | e^{\lambda_n t} \underline v_n)$.

Eqivalentemente, l’integrale generale è $\underline y_0(t) = C_1 e^{\lambda_1 t} \underline v_1 + \dots + C_n e^{\lambda_n t} \underline v_n$ con $C_1, \dots, C_n \in \mathbb{R}$.

1.14 Esponenziale di una matrice

Sia $A \in \mathcal{M}_\mathbb{R}(n)$, la matrice esponenziale $e^A$ è definita dalla serie

$$e^A = \sum_{k = 0}^{+ \infty} \frac{A^k}{k!} = I + A + \frac{1}{2} A^2 + \frac{1}{3} A^3 + \dots$$

e risulta convergente $\forall A$.

Se $A$ è diagonalizzabile reale, allora è più semplice calcolare la matrice esponenziale:

$$e^A = S \cdot \text{diag}(e^{\lambda_1} , \dots, e^{\lambda_n}) \cdot S^{-1}$$

ove $S$ è è la matrice ottenuta affiancando gli autovettori di $A$ è i vari $\lambda_i$ sono gli autovalori.

Se $A$ è diagonalizzabile reale allora $e^{At}$ è una matrice wronskiana relativa al sistema omogeneo $\underline y' = A \underline y$ e l’integrale generale di tale sistema si scrive come $\underline y_o = e^{At} \cdot \underline C$ con $\underline C \in \mathbb{R}$.

La matrice esponenziale è comoda per risolvere il problema di Cauchy: dato che $(e^{At_0})^{-1} = e^{-At_0}$, la soluzione del problema di Cauchy è $\underline y(t) = e^{A(t - t_0)}\underline y_0$.

1.15 Risoluzione esplicita di sistemi con $A \in \mathcal{M}_\mathbb{R}(2 )$ con autovalori complessi coniugati

Sia $A \in \mathcal{M}_{\mathbb{R}}(2)$ con autovalori $\lambda$ e $\overline \lambda$ complessi coniugati, $\Im \lambda = 0$ e $\underline v \in \mathbb{C}^2$ autovalore associato a $\lambda$. Un sistema fondamentale di soluzioni di un sistema omogeneo è dato da

$$y_{o1}(t) = \Re (e^{\lambda t} \underline v) \qquad y_{o2}(t) = \Im(e^{\lambda t} \underline v)$$

Equivalentemente, l’integrale generale è $y_o(t) = C_1 \Re(e^{\lambda t} \underline v) + C_2 \Im(e^{\lambda t} \underline v)$.

1.16 Sistemi non omogenei

Struttura dell’integrale generale dei sistemi non omogenei:

Siano $A \in \mathcal{M}_\mathbb{R}(n)$ e $b_i : J \sube \mathbb{R} \to \mathbb{R}$ continue. L’integrale generale del sistema differenziale lineare completo $\underline y'(t) = A \underline y(t) + \underline b(t)$ è $\underline y(t) = \underline y_o(t) + \underline y_p(t)$ dove $\underline y_o(t)$ è la soluzione del sistema omogeneo associato e $\underline y_p(t)$ è una soluzione particolare.

Sia $\underline y' = A \underline y$ e $A \in \mathcal{M}_\mathbb{R}(2)$. Se il sistema ha soluzioni periodiche allora $A$ non è diagonalizzabile reale.

Per risolvere un sistema completo $\underline y'(t) = A \cdot \underline y(t) + \underline b(t)$, prima di tutto si risolve il sistema omogeneo associato trovando la matrice wronskiana (tornerà utile nei passaggi successivi):

$$W(t) = (\underline y_{o1}(t) | \dots | \underline y_{on}(t)) \\ \underline y_o(t) = W(t) \cdot \underline C \qquad \underline C \in \mathbb{R}$$

Poi si procede calcolando l’integale generale utilizzando la seguente formula:

$$\underline y(t) = W(t) \cdot \left( \int \left[ W(\tau)^{-1} \right] \cdot \underline b(\tau) d \tau + \underline C \right) = \underbrace{W(t) \cdot \int \left[ W(\tau)^{-1} \right] \cdot \underline{b}(\tau) d\tau}_{\underline y_p(t)} + \underbrace{W(t) \cdot \underline C}_{\underline y_o(t)} \qquad \underline C \in \mathbb{R}$$

In questa formula, per integrale di un vettore, si intende vettore di integrali, componente per componente.

Ricordando le proprietà dell’esponenziazione di matrici, nel caso specifico in cui $A$ è diagonalizzabile, è possibile scegliere come matrice wronskiana $W(t) = e^{At}$, semplificando la formula e rendendola formalmente identica alla formula per le EDO del primo ordine lineari:

$$\underline y(t) = e^{At} \left( \int e^{-A\tau} \cdot \underline b(\tau) d \tau + \underline C \right) \qquad \underline C \in \mathbb{R}$$

Si semplifica anche la risoluzione del problema di Cauchy:

$$\underline y(t) = e^{A(t - t_0)} \cdot \int_{t_0}^t e^{-A \tau} \cdot \underline b(\tau) d \tau + e^{A(t - t_0)} \underline y(t_0)$$

Capitolo Due: Serie di funzioni

Siano $f_n : J \sube \mathbb{R} \to \mathbb{R}$ con $n=0, 1, \dots$, allora la serie di funzioni di termine generale $f_n$ è la successione delle somme parziali

$$\begin{align*} S_0(x) = & f_0(x) \\ S_1(x) = & f_0(x) + f_1(x) \\ \vdots & \\ S_k(x) = & \sum_{n = 0}^k f_n(x) \end{align*}$$

Fissato un $\overline x \in J$, si ottiene una serie numerica.

Diciamo che una serie converge puntualmente o semplicemente nel punto $\overline x \in J$ se la serie numerica di termine generale $f_n(\overline x)$ è convergente, ovvero esiste finito il seguente limite:

$$\lim_{k \to +\infty} S_k(\overline x) = \lim_{k \to \infty} \sum_{n = 0}^{k} f_n(\overline x)$$

Notare che, per una stessa funzione, questo limite potrebbe convergere per alcuno $\overline x$ e divergere o essere indeterminato per altri $\overline x$.

E’ detto insieme di convergenza puntuale il sottoinsieme $E \sube J$ di punti nei quali la serie converge (quindi dove il limite esiste finito).

La funzione somma della serie è una funzione $f : E \to \mathbb{R}$ definita come

$$f(x) = \sum_{n = 0}^{+ \infty} f_n(x) = \lim_{k \to + \infty} S_k(x)$$

La serie di termine generale $f_n(x)$ con $x \in J$ converge assolutamente in $\overline x \in J$ se la serie numerica di termine generale $|f_n(\overline x)|$ è convergente.

Per la convergenza assoluta, se $|f_n(\overline x)|$ converge, allora anche $-|f_n(\overline x)|$ converge. Per il teorema del confronto (noto anche come t. dei carabinieri, t. degli sbirri, t. del sandwich e t. di compressione), dato che $- |f_n(\overline x)| \le f_n(\overline x) \le |f_n(\overline x)|$ allora anche $f_n(\overline x)$ converge. Ne segue che la convergenza assoluta implica la convergenza semplice ma non vale l’opposto.

Diciamo che la serie di termine generale $f_n(x)$ con $x \in J$ converge totalmente nell’intervallo non vuoto $I \sube J$ (detto insieme di convergenza totale) se esiste una successione numerica $a_n \ge 0$ tale che $|f_n(x)| \le a_n \ \forall x \in I, \forall n = 0, 1, 2, \dots$ e che $\sum_{n=0}^{+\infty} a_n \lt + \infty$ (cioè $a_n$ convergente).

La convergenza totale in $I \sube J$ implica la convergenza assoluta e puntuale $\forall x \in I$ e la convergenza totale in ogni sottoinsieme non vuoto di $I$.

2.1 Teorema di continuità della somma

Siano $f_n$ funzioni definite almeno in un intervallo $I \sube R$. Se le funzioni sono continue in $I$ e la serie generale converge totalmente in $I$ allora la funzione somma è continua in $I$.

2.2 Teorema di integrabilità termine a termine

Nelle stesse ipotesi del teorema precedente, per un qualunque intervallo $[c, d] \sub I$ chiuso e limitato, si ha che la funzione somma $f$ è integrabile e vale che

$$\int_c^d f(x) dx = \int_c^d \left( \sum_{n=0}^{+\infty} f_n(x) \right) dx = \sum_{n=0}^{+\infty} \int_c^d f_n(x) dx$$

Se le $f_n$ sono derivabili in $I$, $\sum f_n$ converge totalmente in $I$ e $\sum f'_n$ converge totalmente in $I$ allora è possibile derivare termine a termine:

$$f' = \left( \sum_{n=0}^{+\infty} f_n \right)' = \sum_{n=0}^{+\infty} f'_n$$

2.3 Serie di potenze

Una serie di potenze è una serie numerica della forma

$$\sum_{n=0}^{+\infty} a_n(x - x_0)^n$$

dove $a_n \in \mathbb{R}$ vengono detti coefficienti della serie e $x_0 \in \mathbb{R}$ è il centro della serie.

Nella seguente sezione, si considera $(x_0 - x_0)^0 = 1$.

Per $x = x_0$ si ha che

$$\sum_{n=0}^{+\infty} a_n(x_0 - x_0)^n = a_0 \cdot 1 + a_1 \cdot 0 + a_2 \cdot 0 + \dots = a_0$$

Ne segue che tutte le serie di potenze convergono nel loro centro.

L’insieme di convergenza di una serie di potenze è sempre un intervallo centrato in $x_0$ (eventualmente solo $x_0$ o tutto $\mathbb{R}$).

Il raggio di tale intervallo è detto raggio di convergenza.

Teorema del calcolo del raggio di convergenza

Data la serie di potenze

$$\sum_{n=0}^{+\infty} a_n(x - x_0)^n$$

esiste almeno uno dei seguenti due limiti (che può essere eventualmente nullo o infinito), allora il raggio di convergenza è esattamente pari al risultato di tale limite:

$$R = \lim_{n \to +\infty} \left| \frac{a_n}{a_{n+1}} \right| \qquad R = \lim_{n \to +\infty} \frac{1}{\sqrt[n]{|a_n|}}$$

Il primo di questi limiti viene detto criterio del rapporto mentre il secondo viene detto criterio della radice.

Se entrambi i limiti esistono finiti, il risultato allora corrisponde.

E’ possibile osservare che data una serie a termini positivi $\sum a_n$ e $l = \frac{1}{R}$ allora se $l \lt 1$ si ha convergenza e se $l \gt 1$ no.

La convergenza di $\sum a_n$ e quella di $\sum a_n(x - x_0)^n$ non sono correlate in alcun modo.

Dimostrazione

La serie di potenze $\sum a_n(x - x_0)^n$ converge assolutamente in $\overline x$ se la serie numerica $\sum |a_n| |\overline x - x_0|^n = \sum b_n$ converge.

Questa è una serie numerica a termini positivi per cui posso scegliere se applicare il criterio del rapporto o quello della radice.

Se il criterio del rapporto è applicabile, la serie converge se

$$\begin{align*} \lim_{n \to +\infty} \frac{b_{n+1}}{b_n} \lt 1 \iff & \lim_{n \to +\infty} \frac{|a_{n+1}|}{|a_n|} \frac{|\overline x - x_0|^{n+1}}{|\overline x - x_0|^n} \lt 1 \\ \iff & \lim_{n \to +\infty} \frac{|a_{n+1}|}{|a_n|} |\overline x - x_0| \lt 1 \\ \iff & |\overline x - x_0| \lim_{n \to +\infty} \frac{|a_{n+1}|}{|a_n|} \lt 1 \\ \iff & |\overline x - x_0| \lt \frac{1}{\lim_{n \to +\infty} \frac{|a_{n+1}|}{|a_n|}} = \lim_{n \to +\infty} \frac{|a_n|}{|a_{n+1}|} = R \end{align*}$$

Se il criterio della radice è applicabile, la serie converge se

$$\begin{align*} \lim_{n \to +\infty} \sqrt[n]{b_n} \lt 1 \iff & \lim_{n \to +\infty} \left( |a_n| |\overline x - x_0|^n \right)^{\frac{1}{n}} \lt 1 \\ \iff & \lim_{n \to +\infty} \left( |a_n|^{\frac{1}{n}} |\overline x - x_0| \right) \lt 1 \\ \iff & |\overline x - x_0| \lim_{n \to +\infty} |a_n|^{\frac{1}{n}} \lt 1 \\ \iff & |\overline x - x_0| \lt \frac{1}{\lim_{n \to +\infty} |a_n|^{\frac{1}{n}}} = \lim_{n \to +\infty} \frac{1}{|a_n|^{\frac{1}{n}}} = \lim_{n \to +\infty} \frac{1}{\sqrt[n]{|a_n|}} \end{align*}$$

Se $0 \lt R \lt + \infty$ la serie converge totalmente in ogni intervallo chiuso $[c, d] \sube (x_0 - R, x_0 + R)$ (in questo caso, la convergenza è totale in $[c, d] \sub (x_0 - R, x_0 + R)$ ma non necessariamente totale anche in tutto $(x_0 - R, x_0 + R)$).

Se $R = +\infty$ (cioè la $\sum$ converge assolutamente $\forall x \in \mathbb{R}$) allora la convergenza è totale per tutti gli intervalli limitati (in questo caso la convergenza è totale su tutti i limitati ma non necessariamente sull’intero $\mathbb{R}$).

In pratica, per calcolare il raggio di convergenza di una serie definita come $\sum a_n(x - x_0)^n$, considero la serie $\sum a_n$ e ne calcolo il limite con il criterio del rapporto o della radice (come in analisi I) è il reciproco di tale limite è il raggio di convergenza.

Teorema di integrabilità termine a termine

Data una serie $\sum a_n(x - x_0)^n$ con raggio di convergenza $0 \lt R \le + \infty$, per ogni $x \in (x_0 - R, x_0 + R)$ finito, vale la formula di integrazione termine a termine:

$$\int_{x_0}^x \sum_{n=0}^{+\infty} a_n(t - x_0)^n dt = \sum_{n=0}^{+\infty} a_n \int_{x_0}^x (t - x_0)^n dt = \sum_{n=0}^{+\infty} \frac{a_n}{n+1} (x - x_0)^{n+1}$$

La serie di potenze integrata mantiene lo stesso raggio di convergenza infatti sia $b_n = \frac{a_n}{n+1}$, allora

$$\lim_{n \to +\infty} \left| \frac{b_n}{b_{n+1}} \right| = \lim_{n \to +\infty} \left| \frac{a_n}{n+1} \frac{n + 2}{a_{n+1}} \right| = \lim_{n \to +\infty} \left[ \frac{n + 2}{n + 1} \left| \frac{a_n}{a_{n+1}} \right| \right] = \lim_{n \to +\infty} \left| \frac{a_n}{a_{n + 1}} \right| = R$$

Teorema di derivabilità termine a termine

Nelle stesse ipotesi del teorema precedente, vale la formula di derivabilità termine a termine:

$$\left[ \sum_{n=0}^{+\infty} a_n(x - x_0)^n \right]' = \sum_{n=1}^{+\infty} na_n(x - x_0)^{n - 1}$$

Anche in questo caso la serie derivata ha raggio di convergenza $R$.

Questa formula può essere iterata per ottenere serie derivate di ogni ordine, tutte con raggio di convergenza $R$.

Non è detto che una serie di potenze converga negli estremi dell’intervallo di convergenza.

Integrando una serie, se in un estremo convergeva, allora la serie integrata rimarrà convergente in tale estremo mentre se non era convergeva potrebbe diventare convergente.

Derivando una serie si ottiene il comportamento opposto: se la serie potrebbe perdere la convergenza negli estremi ma se in un estremo era già divergente, allora rimarrà divergente.

Ne segue che il comportamento negli estremi va studiato a parte.

2.4 Criterio di Leibniz

Come in Analisi I, per le serie di potenze reali, vale il criterio di Leibniz: per $\sum a_n$, $a_n = (-1)^nb_n$ con $b_n \gt 0$, arrestando la somma al termine $a_n$, si commette un errore minore a $|a_{n+1}|$.

Capitolo Quattro: Serie di Taylor

Una funzione è detta analitica reale se nell’intervallo non vuoto $(a, b)$ è somma di una serie di potenze in $(a, b)$, quindi se

$$\exists x_0 \in (a, b), \exists a_n \in \mathbb{R} : f = \sum_{n=0}^{+\infty} a_n(x - x_0)^n \quad \forall x \in (a, b)$$

Se $f$ è analitica in $(a, b)$ allora $f$ è derivabile ad ogni ordine.

I coefficienti $a_n$ sono

$$f(x_0) = \sum_{n=0}^{+\infty} a_n(x_0 - x_0) = a_0 \\ f'(x) = \sum_{n=1}^{+\infty} n a_n(x - x_0)^{n-1} \implies f'(x_0) = a_1 \\ f''(x) = \sum_{n=2}^{+\infty} n^2 a_n (x - x_0)^{n-2} \implies f''(x_0) = 2a_2 \\ \vdots \\ a_n = \frac{f^{(n)}(x_0)}{n!}$$

4.1 Funzioni analitiche reali

Sia $f$ una funzione di una variabile reale, analitica su di un intervallo non vuoto $(a, b)$. Allora $f$ è derivabile ad ogni ordine in $(a, b)$ e $\forall x_0 \in (a, b)$ è sviluppabile in una serie di Taylor:

$$f(x) = \sum_{n=0}^{+\infty} \frac{f^{(n)}(x_0)}{n!}(x - x_0)^n \qquad x \in (a, b)$$

4.2 Serie di potenze complesse

Una serie di potenze complesse è una serie numerica della forma

$$\sum_{n=0}^{+\infty} a_n(z - z_0) = a_0 + a_1(z - z_0) + \dots + a_n(z - z_0)^n \qquad a_n, z, z_0 \in \mathbb{C}$$

Restano valide le formule per il calcolo del raggio di convergenza.

Se $R = 0$ allora la serie converge solo in $z_0$, se $R = +\infty$ la serie converge $\forall z \in \mathbb{C}$ mentre se $0 \lt R \lt +\infty$ allora la serie converge assolutamente $\forall z_0 : |z - z_0| \lt R$ ma non si può dire niente per la frontiera (la serie potrebbe convergere o meno $\forall z_0 : |z - z_0| = R$).

L’esponenziale complesso si calcola come

$$e^z = \sum_{n=0}^{\infty} \frac{z^n}{n!}$$

ed è definito $\forall z \in \mathbb{C}$ dato che $R = +\infty$.

4.3 Serie di Fourier

Con le serie di Fourier, si possono scomporre funzioni non necessariamente analitiche in una serie infinita di funzioni trigonometriche della forma

$$f(x) = a_0 + \sum_{n=1}^{+\infty} \left[ a_n \cos (nx) + b_n \sin (nx) \right]$$

dove gli $a_n$ e i $b_n$ sono detti coefficienti di Fourier.

Per comprendere i successivi argomenti, è necessario avere famigliarità con le proprietà delle funzioni periodiche:

• $f$ è periodica di periodo $T$ se $f(x) = f(x + T)$.
• Se $f$ è periodica di periodo $T$ allora è periodica anche di periodo $kT$ con $k \in \mathbb{N}$.
• Se $f$ è periodica di periodo $T$ ed è pari in $[-\frac{T}{2}, \frac{T}{2}]$ allora è pari in tutto $\mathbb{R}$.
• Una funzione costante è periodica di qualsiasi periodo.

Vengono dette armoniche $n$-esime le funzioni $\cos nx$ e $\sin nx$ che sono periodiche di periodo $\frac{2\pi}{n}$.

Tutte le armoniche $n$-esime sono periodiche di periodo $2 \pi$.

Per il calcolo dei coefficienti di Fourier, è necessario tenere a mente le formule di ortogonalità:

$$\int_{-\pi}^{\pi} \cos(nx) \cos(kx) dx = \begin{cases} 0 & n \ne k \\ \pi & n = k \ne 0 \\ 2\pi & n = k = 0 \\ \end{cases} \\ \int_{-\pi}^{\pi} \sin(nx) \sin(kx) dx = \begin{cases} 0 & n \ne k \\ \pi & n = k \ne 0 \\ 2\pi & n= k = 0 \\ \end{cases} \\ \int_{-\pi}^{\pi} \sin(nx) \cos(nx) = 0 \quad \forall n,k \in \mathbb{R}$$

Un polinomio trigonometrico di ordine $m \in \mathbb{N}$ è una combinazione lineare di armoniche $n$-esime con $n = 1, 2, \dots, m$ della forma

$$a_0 + \sum_{n=1}^{m} \left[ a_n \cos(nx) + b_n \sin(nx) \right]$$

dove $a_0, a_n, b_n$ vengono detti coefficienti del polinomio trigonometrico.

Ogni polinomio trigonometrico è $2\pi$-periodico, così come qualsiasi somma, differenza o prodotto tra essi.

Una serie trigonometrica è una serie della forma

$$a_0 + \sum_{n=1}^{+\infty} \left[ a_n \cos(nx) + b_n \sin(nx) \right]$$

La somma di una serie trigonometrica è $2\pi$-periodica.

Una serie trigonometrica converge totalmente solo quando $|a_n| + |b_n|$ converge, infatti $|f_n(x)| = |a_n \cos(nx) + b_n \sin(nx)| \le |a_n| + |b_n| \quad \forall x \in \mathbb{R}$.

Se

$$\sum_{n=1}^{+\infty} \left[ |a_n| + |b_n| \right] \lt + \infty$$

allora la serie trigonometrica converge totalmente in $\mathbb{R}$. In particolare la funzione somma è continua in tutto $\mathbb{R}$ e vale la formula di integrazione termine a termine in ogni sottoinsieme limitato (non serve richiedere la chiusura dell’insieme dato che, essendo la funzione continua, allora non esploderà in nessun punto).

Inoltre, nella stessa circostanza di quanto appena scritto, la funzione somma è derivabile in tutto $\mathbb{R}$ e vale la formula di derivazione termine a termine.

4.4 Costruzione della serie di Fourier di una funzione periodica

Per calcolare i coefficienti di Fourier per esprimere una funzione periodica come serie di Fourier, ci si basa sul teorema che segue, di cui è fornita anche la dimostrazione.

Il teorema si limita alle funzioni $2\pi$-periodiche; dopo la dimostrazione verranno fornite formule più generali che vanno bene per qualsiasi periodo.

Teorema del calcolo dei coefficienti di Fourier

Sia $f : \mathbb{R} \to \mathbb{R}$ $2\pi$-periodica, e somma di una serie trigonometrica:

$$f(x) = a_0 + \sum_{n=1}^{+\infty} \left[ a_n \cos(nx) + b_n \sin(nx) \right]$$

Supponiamo inoltre di poter integrare termine a termine, allora

$$\begin{align*} a_0 = \frac{1}{2 \pi} \int_{-\pi}^{+\pi} f(x) dx \qquad & a_n = \frac{1}{\pi} \int_{-\pi}^{+\pi} f(x) \cos(nx) dx \quad n \ge 1 \\ & b_n = \frac{1}{\pi} \int_{-\pi}^{+\pi} f(x) \sin(nx) dx \quad n \ge 1 \end{align*}$$

Queste formule valgono anche in caso di convergenza non totale purchè si possa integrare termine a termine.

Dimostrazione

Per calcolare $a_0$ integro $f(x)$ in $(-\pi, \pi)$ sfruttando l’integrabilità termine a termine e le formule di ortogonalità:

$$\begin{align*} \int_{-\pi}^{+\pi} f(x) dx &= \int_{-\pi}^{+\pi} \left[ a_0 + \sum_{n=1}^{+\infty} \left[ a_n \cos(nx) + b_n \sin(nx) \right] \right] dx \\ &= \int_{-\pi}^{+\pi} a_0 dx + \sum_{n=1}^{+\infty} \left[ \int_{-\pi}^{+\pi} a_n \cos(nx) dx \right] + \sum_{n=1}^{+\infty} \left[ \int_{-\pi}^{+\pi} b_n \sin(nx) dx \right] \\ &= \int_{-\pi}^{+\pi} a_0 dx + \sum_{n=1}^{+\infty} \left[ a_n \underbrace{\int_{-\pi}^{+\pi} \cos(nx) dx}_{=0} \right] + \sum_{n=1}^{+\infty} \left[ b_n \underbrace{\int_{-\pi}^{+\pi} \sin(nx) dx}_{=0} \right] \\ &= 2\pi a_0 \implies a_0 = \frac{1}{2\pi} \int_{-\pi}^{+\pi} f(x) dx \end{align*}$$

Per determinare $a_n$, moltiplico $f(x)$ per $\cos(nx)$, integro su $(-\pi, \pi)$ utilizzando ancora una volta l’integrabilità termine a termine e le formule di ortogonalità:

$$\begin{align*} \int_{-\pi}^{+\pi} f(x) \cos(nx) dx &= \int_{-\pi}^{+\pi} \left[ a_0 + \sum_{k=1}^{+\infty} \left[ a_k \cos(kx) + b_k \sin(kx) \right] \right]\cos(nx) dx \\ &= \int_{-\pi}^{+\pi} a_0 \cos(nx) dx + \sum_{k=1}^{+\infty} \left[ \int_{-\pi}^{+\pi} a_k \cos(kx) \cos(nx) dx \right] + \sum_{k=1}^{+\infty} \left[ \int_{-\pi}^{+\pi} b_k \sin(kx) \cos(nx) dx \right] \\ &= a_0 \underbrace{\int_{-\pi}^{+\pi} \cos(nx) dx}_{=0} + \sum_{k=1}^{+\infty} \left[ a_k \underbrace{\int_{-\pi}^{+\pi} \cos(kx) \cos(nx) dx}_{\text{Si annulla se $n \ne k$}} \right] + \sum_{k=1}^{+\infty} \left[ b_k \underbrace{\int_{-\pi}^{+\pi} \sin(kx) \cos(nx) dx}_{=0} \right] \\ &= a_n \int_{-\pi}^{+\pi} \cos(nx)^2 dx = \pi a_n \implies a_n = \frac{1}{\pi}\int_{-\pi}^{+\pi} f(x) \cos(nx) dx \end{align*}$$

Per calcolare i $b_n$ il procedimento è analogo:

$$\begin{align*} \int_{-\pi}^{+\pi} f(x) \sin(nx) dx &= \int_{-\pi}^{+\pi} \left[ a_0 + \sum_{k=1}^{+\infty} \left[ a_k \cos(kx) + b_k \sin(kx) \right] \right] \sin(nx) dx \\ &= \int_{-\pi}^{+\pi}a_0 \sin(nx) dx + \sum_{k=1}^{+\infty} \left[ \int_{-\pi}^{+\pi} a_k \cos(kx) \sin(nx) dx \right] + \sum_{k=1}^{+\infty} \left[ \int_{-\pi}^{+\pi} b_k \sin(kx) \sin(nx) dx \right] \\ &= a_0 \underbrace{\int_{-\pi}^{+\pi} \sin(nx) dx}_{=0} + \sum_{k=1}^{+\infty} \left[ a_k \underbrace{\int_{-\pi}^{+\pi} \cos(kx) \cos(nx) dx}_{=0} \right] + \sum_{k=1}^{+\infty} \left[ b_k \underbrace{\int_{-\pi}^{+\pi} \sin(kx) \sin(nx) dx}_{\text{Si annulla se $n \ne k$}} \right] \\ &= b_n \int_{-\pi}^{+\pi} \sin(nx)^2 dx = \pi b_n \implies b_n = \frac{1}{\pi} \int_{-\pi}^{+\pi} f(x) \sin(nx) dx \end{align*}$$

Come volevasi dimostrare.

Le formule generali che valgono qualsiasi sia il periodo $T$ sono

$$\begin{align*} a_0 = \frac{1}{T} \int_{-\frac{T}{2}}^{+\frac{T}{2}} \qquad & a_n = \frac{2}{T} \int_{-\frac{T}{2}}^{\frac{T}{2}} f(x) \cos \left( n \frac{2 \pi}{T} x \right) dx \\ & b_n = \frac{2}{T} \int_{-\frac{T}{2}}^{\frac{T}{2}} f(x) \sin \left( n \frac{2 \pi}{T} x \right) dx \end{align*}$$

Chiamiamo polinomio di Fourier di ordine $m$ il polinomio trigonometrico

$$F_m(x) = a_0 + \sum_{n=1}^m \left[ a_n \cos(nx) + b_n \sin(nx) \right]$$

Chiamiamo serie di Fourier la serie trigonometrica

$$\lim_{m \to \infty} F_m(x) = a_0 + \sum_{n=1}^{+\infty} \left[ a_n \cos(nx) + b_n \sin(nx) \right]$$

E’ possibile semplificare il calcolo dei coefficienti di Fourier andando a sfruttare alcune proprietà della funzione sotto analisi:

• se la funzione è pari allora si sviluppa solo il coseno ($b_n = 0 \quad \forall n$)
• se la funzione è dispari allora si sviluppa solo il seno ($a_n = 0 \quad \forall n$)
• nei punti in cui la funzione è discontinua, la sommatoria nel polinomio vale zero

Per studiare la convergenza della serie di Fourier, è necessario introdurre alcuni concetti.

Una funtione $f : [-\pi, +\pi] \to \mathbb{R}$ è regolare a tratti nell’intervallo $[-\pi, +\pi]$ se esiste un numero finito di punti $-\pi \lt x_1 \lt x_2 \lt \dots \lt x_n \lt +\pi$ tali per cui $f$ è derivabile in in ogni intervallino $(x_i, x_{i+1})$ ed esistono finiti i limiti

$$\lim_{x \to x_i^+} f(x) \quad \forall i = 1, 2, \dots, n-1 \qquad \lim_{x \to x_i^-} f(x) \quad \forall i = 2, 3, \dots, n$$

Ovviamente, se $f$ è periodica e regolare a tratti su un dato intervallo allora è regolare a tratti ed è integrabile in qualunque intervallo limitato.

Sia $f : \mathbb{R} \to \mathbb{R}$ $2\pi$-periodica e regolare a tratti in $[-\pi, +\pi]$ allora la serie di Fourier di $f$ converge puntualmente $\forall x \in \mathbb{R}$ e inoltre

$$\lim_{m \to \infty} F_m(x) = \frac{1}{2} \left( \lim_{S \to x^+} f(S) + \lim_{S \to x^-} f(S) \right)$$

cioè nei punti di discontinuità-salto, il polinomio di Fourier converge alla metà tra i due punti del salto.

Se $f$ è continua, allora $\lim_{m \to \infty} F_m(x) = f(x)$ che si può anche scrivere come $\lim_{m \to \infty} \left| F_m(x) - f(x) \right| = 0$.

Ne segue che se $f : \mathbb{R} \to \mathbb{R}$ è anche $2\pi$-periodica, regolare a tratti in $[-\pi, +\pi]$ e continua in tutto $\mathbb{R}$ allora si ha che la serie di Fourier di $f$ converge totalmente a $f$.

Sia $f : \mathbb{R} \to \mathbb{R}$, $2\pi$-periodica e regolare a tratti in $[-\pi, +\pi]$ allora vale la convergenza in media quadratica:

$$\lim_{m \to +\infty} \int_{-\pi}^{+\pi} \left( F_m(x) - f(x) \right)^2 dx = 0$$

Ciò implica che

$$\lim_{m \to +\infty} \int_{-\pi}^{+\pi} F_m(x)^2 dx = \int_{-\pi}^{+\pi} f(x)^2 dx$$

Tale formula in realtà vale per qualsiasi intervallo $[c, d]$ se la $f$ è periodica, in quanto se $[c, d] \sube [-\pi, +\pi]$ allora è ovvio, altrimenti si ragiona per periodicità.

Si può dunque calcolare

$$\int_{-\pi}^{+\pi} F_m(x)^2 dx = \int_{-\pi}^{+\pi} \left( a_0 + \sum_{n=1}^{m} (a_n \cos(nx) + b_n \sin(nx)) \right)^2 dx = 2\pi a_0^2 + \pi \sum_{n=1}^{m} (a_n^2 + b_n^2)$$

Facendo tendere $m$ all’infinito, si arriva all’identità di Bessel-Parsival:

$$\frac{1}{\pi} \int_{-\pi}^{+\pi} f(x)^2 dx = 2 a_0^2 + \sum_{n=1}^{+\infty} (a_n^2 + b_n^2)$$

Cenni alla forma esponenziale

Conoscendo le formule di Eulero,

$$\cos x = \frac{e^{ix} + e^{-ix}}{2} \qquad \sin x = \frac{e^{ix} - e^{-ix}}{2i}$$

possiamo dire che

$$\cos nx = \frac{e^{inx} + e^{-inx}}{2} \qquad \sin x = \frac{e^{inx} - e^{-inx}}{2i}$$

Dunque si può riscrivere la serie trigonometrica

$$\begin{align*} a_0 + \sum_{n=1}^{+\infty} \left[ a_n \cos nx + b_n \sin nx \right] &= a_0 + \sum_{n=1}^{+\infty} \left[ a_n \frac{e^{inx} + e^{-inx}}{2} + b_n \frac{e^{inx} - e^{-inx}}{2i} \right] \\ &= a_0 + \sum_{n=1}^{+\infty} e^{inx} \left( \frac{a_n}{2} + \frac{b_n}{2i} \right)+ \sum_{n=1}^{+\infty} e^{-inx} \left( \frac{a_n}{2} - \frac{b_n}{2i} \right) \\ &= a_0 + \sum_{n=1}^{+\infty} e^{inx} \left( \frac{a_n - ib_n}{2} \right) + \sum_{n=1}^{+\infty} e^{-inx} \left( \frac{a_n + ib_n}{2} \right) \\ &= \underbrace{a_0}_{=c_0} + \sum_{n=1}^{+\infty} e^{inx} \underbrace{\frac{a_n - ib_n}{2}}_{=c_n} + \sum_{k = -\infty}^{-1} e^{ikx} \underbrace{\frac{a_{-k} + ib_{-k}}{2}}_{=c_k} \\ &= c_0 + \sum_{n=1}^{+\infty} c_n e^{inx} + \sum_{k=-\infty}^{-1} c_k e^{ikx} \\ &= \sum_{n = -\infty}^{+\infty} C_n e^{inx} \implies c_n = \frac{1}{2\pi} \int_{-\pi}^{+\pi} f(x) e^{-inx}dx \end{align*}$$

Capitolo Cinque: Cenni di topologia in $\mathbb{R}$

Si dice intorno sferico o palla di raggio $r$ e centro in $\underline x_0 \in \mathbb{R}$ il seguente insieme:

$$B_r(\underline x_0) = \left\{ \underline x \in \mathbb{R}^n : \|\underline x - \underline x_0\| \lt r \right\}$$

E’ importante notare che un apalla è un insieme aperto per definizione.

Si dice complementare dell’insieme $E$ l’insieme $E^C = \mathbb{R}^n - E$.

Dati un insieme $E \sub \mathbb{R}^n$ e un punto $\underline x_0 \in \mathbb{R}^n$ allora

• $\underline x_0$ è di frontiera o di bordo per $E$ se $\forall r \gt 0$ vale che $B_r(\underline x_0) \cap E \ne \emptyset$ e che $B_r(\underline x_0) \cap E^C \ne \emptyset$.
• $\underline x_0$ è interno ad $E$ se $\underline x_0 \in E$ e $\exists r \gt 0 : B_r(x_0) \sub E$.
• $\underline x_0$ è esterno ad $E$ se $\underline x_0$ è interno a $E^C$.

Un insieme $E \sub \mathbb{R}^n$ si dice aperto se $\forall \underline x \in E$ si ha che $\underline x$ è punto interno. Lo stesso insieme è chiuso se $E^C$ è aperto.

Un insieme $E$ si dice limitato se esiste un $r$ tale per cui tutto l’insieme è contenuto in una palla di raggio $r$; è illimitato altrimenti.

Un insieme chiuso e limitato è detto compatto.

5.1 Curve

Una curva in $\mathbb{R}^3$ può essere descritta attraverso la sua parametrizzazione o attraverso il suo sostegno.

La parametrizzazione di una curva consiste essenzialmente in 3 funzioni continue, dipendenti da un solo parametro:

$$\underline r : I \sube \mathbb{R} \to \mathbb{R}^3 \\ \underline r(t) = \begin{pmatrix} r_1(t) \\ r_2(t) \\ r_3(t) \end{pmatrix}$$

Il sostegno della curva consiste nell’insieme di tutti i valori che la curva può assumere:

$$\gamma = \left\{ (x_1, x_2, x_3) \in \mathbb{R}^3 : (x_1, x_2, x_3) = (r_1(t), t_2(t), r_3(t)) \text{ per qualche $t \in I$}\right\}$$

Il sostegno di una curva è univocamente determinato dalla parametrizzazione ma esistono infinite parametrizzazioni associate allo stesso sostegno.

Nel caso in cui $r_3(t) = 0 \quad \forall t$, la curva viene detta curva piana.

E’ possibile ottenere, per una funzione $f$ generica una parametrizzazione

$$\underline r(t) = \begin{pmatrix} t \\ f(t) \end{pmatrix}$$

Due parametrizzazione $\underline r(t) : I \to \mathbb{R}^n$ e $\underline v(s) : J \to \mathbb{R}^n$ si dicono equivalenti se esiste una mappa $\varphi : J \to I$ continua e biunivoca tale che

$$\underline v(s) = \underline r(\varphi(s)) = \underline r \cdot \varphi(s)$$

In pratica, due parametrizzazioni sono equivalenti se hanno lo stesso sostegno, percorso lo stesso numero di volte.

Dato che $\varphi$ è biunivoca, allora è monotona: se è decrescente allora il senso di percorrenza dei due sostegni si inverte.

Una curva può essere considerata come la classe di equivalenza associata che contiene tutte le parametrizzazioni equivalenti.

Una curva si dice regolare se ammette una parametrizzazione $(r_1(t), \dots, r_n(t))$ con $t \in I$ tale per cui tutte le $r_i(t) \in \mathcal{C}^1(I)$ e $(r_1'(t), \dots, r_n'(t)) \ne \underline 0$ per ogni $t$. Se una curva è regolare allora $\|\underline r'(t)\| \ne 0$.

Una curva di dice semplice se è iniettiva, ovvero se il suo sostegno non si interseca con se stesso: se $\exists t_1, t_2 : t_1 \ne t_2, \underline r(t_1) = \underline r(t_2)$ allora la curva non è semplice.

Se $\underline r : I \to \mathbb{R}^3$, si definisce versore tangente il versore

$$\underline T(t) = \frac{\underline r'(t)}{\|\underline r'(t)\|}$$

Il versore tangente ha direzione della retta tangente alla curva nel punto $\underline r(t)$, norma unitaria e verso concorde al verso di percorrenza della curva.

Data una funzione $f \in \mathcal{C}^1$ qualsiasi, una curva costruita come

$$\underline r(t) = \begin{pmatrix} t \\ f(t) \end{pmatrix}$$

è sempre regolare infatti

$$\underline r'(t) = \begin{pmatrix} 1 \\ f'(t) \end{pmatrix}$$

Siano $[a,b] \sube \mathbb{R}$ limitato e $\underline r : [a,b] \to \mathbb{R}$ la parametrizzazione di una curva regolare avente sostegno $\gamma$, allora la lunghezza di $\gamma$ si calcola come

$$\text{len}(\gamma) = \int_a^b \|\underline r'(t)\| dt$$

Siano $[a,b] \sub \mathbb{R}$ limitato e $\underline r : [a,b] \to \mathbb{R}^3$ parametrizzazione di una curva regolare avente sostegno $\gamma$. Se $\underline v[c,d] \to \mathbb{R}^3$ e $\underline v(s) = \underline r \cdot \varphi(s)$ è una parametrizzazione equivalente avente sostegno $\delta$ allora $\text{len}(\delta) = \text{len}(\gamma)$. Dimostrazione a seguire.

Per definizione

$$\text{len}(\gamma) = \int_a^b \|\underline r'(t)\| dt \qquad \text{len}(\delta) = \int_c^d \|\underline v'(s)\| ds$$

Se

$$\underline v(s) = \begin{pmatrix} r_1(\varphi(s)) \\ r_2(\varphi(s)) \end{pmatrix}$$

allora

$$\underline v'(s) = \begin{pmatrix} r_1'(\varphi(s)) \cdot \varphi'(s) \\ r_2'(\varphi(s)) \cdot \varphi'(s) \end{pmatrix} = \varphi'(s) \cdot \begin{pmatrix} r_1'(\varphi(s)) \\ r_2'(\varphi(s)) \end{pmatrix}$$

da cui

$$\| \underline v'(s) \| = |\varphi'(s)| \cdot \| \underline r'(\varphi(s)) \|$$

quindi

$$\text{len}(\delta) = \int_c^d |\varphi'(s)| \cdot \|\underline r'(\varphi(s))\| ds$$

Siccome $\varphi$ è biunivoca, allora è monotona e si può togliere il valore assoluto: $\varphi' \lt 0$ p $\varphi' \gt 0$.

Supponiamo che $\varphi'(s) \ge 0 \quad \forall s \in [c, d]$, allora

$$\text{len}(\delta) = \int_c^d \varphi'(s) \|\underline r'(s)\| ds$$

Applico ora il seguente cambio di variabili: $t = \varphi(s)$, $dt = \varphi'(s) ds$.

Per gli estremi di integrazione si ha che $\varphi : [c,d] \to [a,b]$, $\varphi(c) = a$ e $\varphi(d) = b$ e quindi

$$\text{len}(\delta) = \int_a^b \|\underline r'(t)\| dt = \text{len}(\gamma)$$

Se invece $\varphi'(s) \le 0$ allora

$$\text{len}(\delta) = - \int_c^d \varphi'(s) \| \underline r'(\varphi(s)) \| ds$$

Se applico il cambiamento di variabili $t = \varphi(s)$, $dt = \varphi'(s) ds$ allora, essendo $\varphi' \lt 0$ si ha che $\varphi(c) = b$ e $\varphi(d) = a$ per cui

$$\text{len}(\delta) = -\int_b^a \|\underline r'(t)\| dt = \int_a^b \| \underline r'(t) \| dt = \text{len}(\gamma)$$

I vari integrali, in caso di curva regolare a tratti, sono da intendersi come somma degli integrali dei vari tratti.

Una curva $\underline r : I \to \mathbb{R}^3$ si dice regolare a tratti se è continua su $I$ e la curva è regolare su $I$ tranne che su un numero finito di punti. La lunghezza di una curva regolare a tratti è la somma delle lunghezze dei vari tratti.

Siano $[a,b] \sub \mathbb{R}$ limitato, $\underline r : [a,b] \to \mathbb{R}$ curva regolare di sostegno $\gamma$, $f(\underline r(t))$ continua $\forall t \in [a,b]$, l’integrale curvilineo di $f$ lungo $\gamma$ è

$$\int_\gamma f ds = \int_a^b f(\underline r(t)) \|\underline r'(t)\| dt$$

Capitolo Sei: Funzioni di due variabili

Una funzione di due variabili reali $f : A \sube \mathbb{R}^2 \to \mathbb{R}$ è una relazione che associa ad ogni $(x, y) \in \mathbb{R}$ un unico valore reale $f(x, y) \in \mathbb{R}$.

E’ detto insieme di livello di $f$ al livello $k$ è

$$I_k = \left\{ (x, y) \in A : f(x, y) = k \right\}$$

che è una curva piana.

6.1 Limite multivaraibile

Siano $a \sube \mathbb{R}^2$ aperto, $x_0 \in A$, $f : A \backslash \{\underline x_0\} \to \mathbb{R}$. Diciamo che $f$ tende al limite $l \in \mathbb{R}$ per $\underline x \to \underline x_0$ e scriviamo che $\lim_{\underline x \to \underline x_0} f(x) = l$ se

$$\forall \varepsilon \gt 0 \ \exists \delta \gt 0 : \underline x \in B_\delta(\underline x_0) \backslash \{ \underline x_0 \} \implies |f(\underline x) - l| \lt \varepsilon$$

Per stabilire che un limite non esiste, devo esibire due curve che mandano la funzione in valori diversi quando si fa tendere tale funzione nel punto limite.

6.2 Calcolo del limite con coordinate polari

La procedura di seguito è valida solo per limiti che tendono a $\underline 0$. In caso di limiti che non tendono a $\underline 0$, si transla la funzione.

1. Trovo un candidato limite: ad esempio, se la funzione è identicamente nulla sugli assi cartesiani, il candidato limite è $l = 0$.
2. Scrivo la funzione $g(r, \theta)$ come $f(x, y)$ in coordinate polari, applicando la seguente trasformazione: $$\begin{cases} x = r \cos(\theta) \\ y = r \sin (\theta) \end{cases}$$
3. Cerco una funzione $h(r)$ tale che
   1. $|g(r, \theta) - l| \lt h(r)$;
   2. $\lim_{r \to 0} h(r) = 0$.
4. Se ho trovato la funzione $h$ di cui al punto sopra, allora il candidato limite è il limite che cercavo, altrimenti cambio candidato e riprovo.

Se la funzione sotto esame non è quoziente di polinomi o radici, prima di iniziare la procedura, applico i limiti notevoli.

Il metodo dei limiti notevoli è utilizzabile anche per la dimostrazione della non esistenza del limite.

6.3 Continuità

Sia $A \sube \mathbb{R}^2$ aperto, $f : A \to \mathbb{R}$, $\underline x_0 \in A$. $f$ è continua in $\underline x_0$ se

$$\lim_{\underline x \to \underline x_0} f(x) = f(\underline x_0)$$

$f$ è continua in un insieme se è continua in tutti i punti dell’insieme.

Tutte le funzioni elementari (1-dimensionali) sono continue sul loro insieme di definizione. Quando le si compone per ottenere una funzione 2-dimensionale, l’insieme di definizione della funzione ottenuta è l’intersezione delle funzioni utilizzate per la composizione.

Da ciò segue che la continuità di funzioni 2-dimensionali va verificata solamente nel caso di funzioni definite a tratti.

6.4 Derivate parziali e gradienti

Sia $A \sube \mathbb{R}^2$ aperto, $f : A \to \mathbb{R}$, $(x_0, y_0) \in A$. Le derivate parziali di $f$ in $(x_0, y_0)$ sono

$$\frac{\partial f}{\partial x} (x_0, y_0) = \lim_{h \to 0} \frac{f(x_0 + h, y) - f(x_0, y_0)}{h} \qquad \frac{\partial f}{\partial y}(x_0, y_0) = \lim_{h \to 0} \frac{f(x_0, y_0 + h) - f(x_0, y_0)}{h}$$

Se entrambi i limiti esistono finiti allora $f$ è detta derivabile in $(x_0, y_0)$.

Se $f$ è derivabile, allora è possibile definire la funzione gradiente:

$$\nabla f(x_0, y_0) = \begin{pmatrix} \frac{\partial f}{\partial x} (x_0, y_0) \\ \frac{\partial f}{\partial y} (x_0, y_0) \end{pmatrix}$$

Per calcolare le derivate parziali, derivo una variabile per volta, considerando tutte le altre come se fossero costanti.

E’ necessario usare la definizione per calcolare le derivate parziali quando la funzione sotto esame è definita per casi o quando nella definizione di tale funzione compare $t^\alpha$ con $\alpha \in (0, 1)$ o $|t|^\alpha$ con $\alpha \in (0, 1]$. In tutti gli altri casi, $f$ è sempre derivabile.

6.5 Differenziabilità e piano tangente

Siano $A \sube \mathbb{R}^2$ aperto (aperto perchè serve poter fare i limiti), $f : A \to \mathbb{R}$, allora diciamo che $f$ è differenziabile in $\underline x_0 \in A$ se $f$ è derivabile in $\underline x_0$ e se

$$f(\underline x_0 + \underline h) = f(\underline x_0) + \lang \nabla f(\underline x_0), \underline h \rang + R(\underline h)$$

dove $R(\underline h) = \small o(\|\underline h\|)$ cioè

$$\lim_{\underline h \to 0} \frac{R(\underline h)}{\|\underline h\|} = 0$$

Per semplificare la verifica della differenziabilità di una funzione, ci si basa sul teorema del differenziale totale che afferma che se $f \in \mathcal{C}^1(A)$ allora $f$ è differenziabile in $A$.

Se $f$ è differenziabile in un punto $\underline x_0 = (x_0, y_0)$ allora il piano tangente al grafico di $f$ in $(x_0, y_0, f(x_0, y_0))$ è

$$z = f(x_0) + \lang \nabla f(\underline x_0), \underline x - \underline x_0 \rang$$

6.6 Differenziabilità $\implies$ continuità

Sia $A \sube \mathbb{R}$ aperto, $\underline x_0 \in A$, $f : A \to \mathbb{R}$ differenziabile in $\underline x_0$. Allora $f$ è continua in $\underline x_0$.

Dimostrazione

Devo dimostrare che

$$\lim_{\underline x \to \underline x_0} f(\underline x) = f(\underline x_0)$$

In mainera equivalente, posso scrivere che

$$\lim_{\underline x \to \underline x_0} |f(\underline x) - f(\underline x_0)| = 0$$

Dato che $f$ è differenziabile, allora

$$f(\underline x) - f(\underline x_0) = \lang \nabla f(\underline x_0), \underline x - \underline x_0 \rang + \small o(\|\underline x - \underline x_0 \|)$$

Dunque

$$\begin{align*} |f(\underline x) - f(\underline x_0)| &= |\lang \nabla f(\underline x_0), \underline x - \underline x_0 \rang| \\ &\le |\lang \nabla f(\underline x_0), \underline x - \underline x_0 \rang| + \small o(\|\underline x - \underline x_0\|) \\ &\le \|\nabla f(\underline x_0)\| \cdot \|\underline x - \underline x_0\| + \small o(\|\underline x - \underline x_0\|) = 0 \end{align*}$$

Ne segue che $0 \le |f(\underline x) - f(\underline x_0)|$, da sui segue che

$$\lim_{\underline x \to \underline x_0} |f(\underline x) - f(\underline x_0)| = 0$$

Come volevasi dimostrare.

Siano $A \sube \mathbb{R}$, $\underline x_0 \in A$, $\underline x_0 = (x_0, y_0)$, $f : A \to \mathbb{R}$, $\underline v = (v_1, v_2)$ e $\|\underline v\| = 1$. La derivata direzionale di $f$ in $\underline x_0$ nella direzione $\underline v$ è

$$\frac{\partial f}{\partial v} = \lim_{t \to 0} \frac{f(x_0 + tv_1, y_0 + tv_2) - f(x_0, y_0)}{t} = \lim_{t \to 0} \frac{f(\underline x_0 + t \underline v) - f(\underline x_0)}{t}$$

E’ importante notare come le derivate parziali sono due casi specifici di derivate direzionali, in particolare sono le derivate direzionali con $\underline v=(1, 0)$ e $\underline v = (0, 1)$.

Il fatto che $f$ sia differenziabile in $\underline x_0$ implica che esistano tutte le derivate direzionali ma non vale il viceversa.

Teorema della formula del gradiente

Siano $A \sube \mathbb{R}$ aperto, $\underline x_0 = (x_0, y_0) \in A$, $f : A \to \mathbb{R}$ differenziabile in $\underline x_0$ allora $f$ ammette derivate direzionali in $\underline x_0$ lungo qualunque direzione $\underline v \in \mathbb{R}$ tale che $\|\underline v\| = 1$ e inoltre

$$\frac{\partial f}{\partial \underline v} = \lang \nabla f(\underline x_0), \underline v \rang$$

Dimostrazione

Devo dimostrare che se $f$ è differenziabile in $\underline x_0$ allora vale che

$$\lim_{t \to 0} \frac{f(\underline x_0 + t \underline v) - f(\underline x_0)}{t} = \lang \nabla f(\underline x_0), \underline v \rang$$

Essendo $f$ differenziabile in $\underline x_0$ allora $f(\underline x_0 + \underline h) - f(\underline x_0) = \lang \nabla f(\underline x_0), \underline h \rang + \small o(\|\underline h\|)$.

Scelgo $\underline h = t \underline v$ con $t \to 0$, divido per $t$ è poi calcolo il limite per $t \to 0$:

$$\begin{align*} &\lim_{t \to 0} \frac{f(\underline x_0 + t \underline v) - f(\underline x_0)}{t} \\ =& \lim_{t \to 0} \left[ \frac{\lang \nabla f(\underline x_0), t \underline v \rang}{t} + \frac{\small o(\|t \underline v\|)}{t} \right] \\ =& \lim_{t \to 0} \left[ \frac{t \lang \nabla f(\underline x_0), \underline v \rang}{t} + \frac{\small o(\|t \underline v\|)}{t} \right] \\ =& \lang \nabla f(\underline x_0), \underline v \rang \end{align*}$$

Come volevasi dimostrare.

E’ importante notare che se la funzione non è definita per casi e non contiene radici o valori assoluti, se $f \in \mathcal{C}^1(\mathbb{R}^2)$, per il teorema del differenziale totale, la $f$ è differenziabile in $\mathbb{R}^2$ e quindi vale la formula del gradiente.

Siano $\underline r$ una curva piana e $f$ differenziabile e regolare, ristretta alla curva $\underline r$. La restrizione di $f$ è la funzione $F(t) = (f \cdot \underline r)(t) = f(\underline r(t)) = f(r_1(t), r_2(t))$.

Se f è differenziabile e $\underline r$ è regolare allora $F'(t) = \lang \nabla f(\underline r(t)), \underline r'(t) \rang = \lang \nabla f(r_1(t), r_2(t)), \begin{pmatrix} r_1'(t) \\ r_2'(t) \end{pmatrix} \rang$.

chiamando $\underline v = \frac{\underline r'(t_0)}{\|\underline r'(t_0)\|}$ e $\underline x_0 = \underline r(t_0)$ allora $F'(t_0) = \lang \nabla f(\underline r(t_0)), \frac{\underline r'(t_0)}{\|\underline r'(t_0)\|} \rang \cdot \|\underline r'(t_0)\| = \|\underline r'(t_0)\| \frac{\partial f}{\partial \underline v} (\underline x_0)$ cioè $F'(t_0)$ è multiplo della derivata direzionale di $f$ nella direzione tangente alla curva in $\underline x_0$.

La derivata direzionale di $f$ nella direzione tangente alla curva di livello è nulla: detto $\underline v$ il versore tangente alla curva di livello al livello $k = f(\underline x_0)$, nel punto $\underline x_0$ stesso, si ha che

$$\frac{\partial f}{\partial \underline v} (\underline x_0) = \lang \nabla f(\underline x_0), \underline v \rang$$

Ne segue che il gradiente è nullo oppure ortogonale a $\underline v$.

Teorema di ortogonalità del gradiente alle curve di livello

Sia $A \sube \mathbb{R}^2$ aperto, $f : A \to R$ differenziabile in $A$ e l’insieme di livello $I_k$ sostegno di una curva regolare di parametrizzazione $\underline r$. Allora $\lang \nabla f(\underline r(t)), \underline r'(t) \rang \le 0 \quad \forall t$.

Dimostrazione

Per ipotesi, $I_k$ coincide con il sostegno della curva regolare $\underline r(t)$ cioè $I_k = \{ r(t) : t \in J\}$. In particolare $f(\underline r(t)) = k \quad \forall t \in J$.

Chiamo $F(t) = f(\underline r(t)) = (f \cdot \underline r)(t)$ con $F : J \to \mathbb{R}$.

Da un lato ho che $F(t) = k \quad \forall t \in J$ e che $F'(t) = 0 \quad \forall t \in J$, dall’altro, per il teorema di derivazione della composta, $F'(t) = \lang \nabla f(\underline r(t)), \underline r'(t) \rang \quad \forall t \in J$ da cui $\lang \nabla f(\underline r(t)), \underline r'(t) \rang = 0 \quad \forall t \in J$, come volevasi dimostrare.

Siano $A \sube \mathbb{R}^2$ aperto, $\underline x_0 \in A$, $f : A \to \mathbb{R}$ differenziabile almeno in $\underline x_0$ e $\nabla f(\underline x_0) \ne 0$. Allora

1. $\forall \underline v \in \mathbb{R}^2 : \|\underline v\| = 1$ si ha che $\left|\frac{\partial f}{\partial \underline v} (\underline x_0)\right| \le \left\| \nabla f(\underline x_0) \right\|$ cioè $-\left\|\nabla f(\underline x_0) \right\| \le \frac{\partial f}{\partial \underline v}(\underline x_0)$
2. Detti $\underline v_{\text{max}} = \frac{\nabla f(\underline x_0)}{\|\nabla f(\underline x_0)\|}$ e $\underline v_{\text{min}} = - \underline v_{\text{max}}$ allora si ha che $$\frac{\partial f}{\partial \underline v_{\text{max}}} (\underline x_0) = \|\nabla f(\underline x_0)\| \qquad \frac{\partial f}{\partial v_{\text{min}}}(\underline x_0) = - \|\nabla f(\underline x_0)\|$$

Capitolo Sette: Ottimizzazione libera

Sia $A \sube \mathbb{R}^2$ aperto, $f : A \to \mathbb{R}$ derivabile. Supponiamo che le derivate parziali di $f$ siano a loro volta derivabili in $A$. Definiamo le derivate parziali seconde come

$$\frac{\partial^2 f}{\partial x^2} = \frac{\partial}{x}\left(\frac{\partial f}{\partial x}\right) \qquad \frac{\partial^2 f}{\partial y \partial x} = \frac{\partial}{\partial y} \left( \frac{\partial f}{\partial x} \right) \qquad \frac{\partial^2 f}{\partial x \partial y} = \frac{\partial}{\partial x} \left( \frac{\partial f}{\partial y} \right) \qquad \frac{\partial^2 f}{\partial y^2} = \frac{\partial}{\partial y}\left( \frac{\partial f}{\partial y} \right)$$

Diciamo che f è derivabile 2 volte se tutte e quattro le derivate seconde esistono; in tal caso le organizziamo nella matrice hessiana:

$$H_f(\underline x_0) = \begin{bmatrix} \frac{\partial^2 f}{\partial x^2} = \frac{\partial}{x}\left(\frac{\partial f}{\partial x}\right) & \frac{\partial^2 f}{\partial y \partial x} = \frac{\partial}{\partial y} \left( \frac{\partial f}{\partial x} \right) \\ \frac{\partial^2 f}{\partial x \partial y} = \frac{\partial}{\partial x} \left( \frac{\partial f}{\partial y} \right) & \frac{\partial^2 f}{\partial y^2} = \frac{\partial}{\partial y}\left( \frac{\partial f}{\partial y} \right) \end{bmatrix} = \begin{bmatrix} \left[ \nabla \left( \frac{\partial f}{\partial x} \right) \right]^T \\ \left[ \nabla \left( \frac{\partial f}{\partial y} \right) \right]^T \\ \end{bmatrix}$$

Per il teorema di Schwarz, se $A \sube \mathbb{R}^2$ e $f \in \mathcal{C}^2(A)$ allora $\frac{\partial^2 f}{\partial y \partial x} = \frac{\partial^2 f}{\partial x \partial y}$ cioè la matrice hessiana è simmetrica e questo può semplificare i calcoli.

Chiamiamo forma quadratica indotta da $H_f(x_0, y_0)$ la funzione $q : \mathbb{R}^2 \to R$ tale che

$$q(h_1, h_2) = \begin{pmatrix} h_1, h_2 \end{pmatrix} H_f(x_0, y_0) \begin{pmatrix} h_1 \\ h_2 \end{pmatrix} = \frac{\partial^2 f}{\partial x^2} h_1^2 + 2 \frac{\partial^2 f}{\partial x \partial y}h_1h_2 + \frac{\partial^2 f}{\partial y^2} h_2^2\\ q(\underline h) = \lang \underline h, h_f(\underline x_0) \cdot \underline h \rang = \underline h^T \cdot H_f(\underline x_0) \cdot \underline h$$

Dalla forma quadratica indotta, si può ricavare la matrice $A = \begin{bmatrix} a & b \\ c & d \end{bmatrix}$ ($q(h_1, h_2) = a h_1^2 + 2bh_1h_2 + ch_2^2$) per poi ricavarne il segno:

$\det A$	$a$	Autovalori	Segno
$\gt 0$	$\gt 0$	$++$	Definita positiva
$\gt 0$	$\lt 0$	$--$	Definita negativa
$=0$	$\gt 0$	$+0$	Semidefinita positiva
$=0$	$\lt 0$	$-0$	Semidefinita negativa
$\lt 0$		$+-$	Indefinita

7.1 Serie di Taylor al secondo ordine

Sia $A \sube \mathbb{R}^2$, $f \in \mathcal{C}^2(A)$. $\forall \underline x_0 \in A$ vale che

$$f(\underline x_0 + \underline h) = f(\underline x_0) + \lang \nabla f(\underline x_0), \underline h \rang + \frac{1}{2} \lang \underline h, H_f(\underline x_0) \cdot \underline h \rang + \small o(\|\underline h\|^2)$$

Equivalentemente se $\underline x = \underline x_0 + h$, lo sviluppo diventa

$$f(\underline x) = f(\underline x_0) + \lang \nabla f(\underline x_0), \underline x -\underline x_0 \rang + \frac{1}{2} \lang \underline x - \underline x_0, H_f(\underline x_0)(\underline x - \underline x_0) \rang + \small o(\|\underline x - \underline x_0\|)$$

Siano $A \sub e\mathbb{R}^2$ un sottoinsieme qualunque e $f : A \to \mathbb{R}$, allora un punto $(x_0, y_0) \in A$ si dice

• punto di massimo locale o relativo per $f$ in $A$ se $\exists \delta \gt 0 : f(\underline x_0) \ge f(x, y) \quad \forall(x, y) \in B_\delta(x_0, y_0)$
• punto di massimo globale o assoluto per $f$ in $A$ se $f(x_0, y_0) \ge f(x, y) \quad \forall(x, y) \in A$
• definisioni analoghe per i minimi.

Se un punto rientra nelle definizioni appena date, allora viene detto punto di estremo o estremante o estremale.

Il teorema di Fermat afferma che con $A \sube \mathbb{R}^2$ aperto e $f : A \to \mathbb{R}$, se $(x_0, y_0)$ è estremo per $f$ allora $\nabla f(x_0, y_0) = \begin{pmatrix} 0 \\ 0 \end{pmatrix}$ e viene detto punto critico.

Se un punto è estremale allora è critico ma non vale il viceversa.

Se un punto è critico ma non estremale, è detto sella.

Nel piano, una funzione può essere simmetrica in molteplici modi:

Descrizione	Simmetria
Pari, rispetto all’origine	$f(-x, -y) = f(x, y)$
Dispari, rispetto all’origine	$f(-x, -y) = -f(x, y)$
Pari, rispetto all’asse y	$f(-x, y) = f(x, y)$
Dispari, rispetto all’asse y	$f(-x, y) = -f(x, y)$
Pari, rispetto all’asse x	$f(x, -y) = f(x, y)$
Dispari, rispetto all’asse x	$f(x, -y) = -f(x, y)$

E’ possibile sfruttare queste simmetrie per semplificare la ricerca dei punti critici riducendo di molto lo spazio di ricerca.

Per determinare (e, successivamente, classificare) i punti critici, trovo tutti i punti nei quali $\nabla f(x, y) = \underline 0$ e tutti i punti di non derivabilità: questi punti sono tutti candidati ad essere critici e quindi vanno studiati.

Teorema del criterio della matrice hessiana

Sia $A \sube \mathbb{R}^2$ aperto (in modo da poter applicare il teorema di Fermat), $f \in \mathcal{C}^2(A)$ (in modo che la matrice hessiana esista) e $\underline x_0 = (x_0, y_0)$ punto critico di $f$ (cioè $\nabla f(x_0, y_0) = 0$). Denoto con $q$ la forma quadratica indotta dalla matrice $H_f(\underline x_0)$:

$$q(h_1, h_2) = (h_1, h_2) \cdot H_f(x_0) \cdot \begin{pmatrix} h_1 \\ h_2 \end{pmatrix}$$

Allora

1. Se $q$ è definita positiva allora $\underline x_0$ è punto di minimo
2. Se $q$ è definita negativa allora $\underline x_0$ è punto di massimo
3. Se $q$ è indefinita allora $\underline x_0$ è punto di sella

Dimostrazione

Essendo per ipotesi $\underline x_0$ un punto critico allora $\nabla f(x_0, y_0) = 0$ e quindi nello sviluppo di Taylor al secondo ordine non compare il gradiente:

$$f(\underline x_0 + \underline h) = f(\underline x_0) + \frac{1}{2} q(\underline h) + \small o(\|\underline h\|)$$

Se $q$ è definita positiva, per definizione $q(\underline h) \gt 0 \quad \forall \underline h \ne \underline 0$ quindi $f(\underline x_0 + \underline h) \gt f(\underline x_0) + \small o(\|\underline h\|)$ quindi $\underline x_0$ è un punto di minimo locale.

Se $q$ è definita positiva, per definizione $q(\underline h) \lt 0 \quad \forall \underline h \ne \underline 0$ quindi $f(\underline x_0 + \underline h) \lt f(\underline x_0) + \small o(\|\underline h\|)$ quindi $\underline x_0$ è un punto di massimo locale.

Se $q$ è indefinita, per definizione $\exists \underline h_1, \underline h_2 : q(\underline h_1) \gt 0, q(\underline h_2) \lt 0$ quindi $f(\underline x_0 + \underline h_1) \gt f(\underline x_0)$ e $f(\underline x_0 + \underline h_2) \lt 0$.

Come volevasi dimostrare.

Se $q$ è indefinita, questo criterio non permette di ricavare informazioni.

Esiste una versione semplificata e più applicabile del precedente teorema:

• Se $\det H_f(x_0, y_0) \gt 0$ e $\frac{\partial^2 f}{\partial x^2}(x_0, y_0) \gt 0$ allora $\underline x_0$ è minimo
• Se $\det H_f(x_0, y_0) \gt 0$ e $\frac{\partial^2 f}{\partial x^2}(x_0, y_0) \lt 0$ allora $\underline x_0$ è massimo
• Se $\det H_f(x_0, y_0) \lt 0$ allora $\underline x_0$ è sella
• Se $\det H_f(x_0, y_0) = 0$ allora bisogna per forza applicare il teorema

Sia $f : \mathbb{R}^2 \to R$, $f \in \mathcal{C}^2(\mathbb{R}^2)$, allora $f$ è convessa in $\mathbb{R}^2$ se $\forall (x, y) \in \mathbb{R}^2$ si ha che $H_f(x, y)$ è definita positiva o semidefinita positiva e $f$ è concava in $\mathbb{R}^2$ se $\forall (x, y) \in \mathbb{R}^2$ si ha che $H_f(x, y)$ è definita negativa o semidefinita negativa.

Se $f \in \mathcal{C}^2(\mathbb{R}^2)$ è convessa e $\underline x_0$ è punto critico allora $\underline x_0$ è punto di minimo assoluto.

Se $f \in \mathcal{C}^2(\mathbb{R}^2)$ è concava e $\underline x_0$ è punto critico allora $\underline x_0$ è punto di massimo assoluto.

Se cerco i punti estremanti di una funzione $f$ in un insieme $A$ non aperto, non è sufficiente applicare il teorema di Fermat nell’aperto perchè potrebbero esserci estremanti sul bordo (e che quindi non verificano il teorema di Fermat).

In tal caso, ci viene in soccorco il teorema di Weierstrass: sia $A \sube \mathbb{R}^2$ chiuso e limitato e sia $f : A \to \mathbb{R}$. Allora $f$ ammette i valori di massimo e minimo assoluto, cioè esistono $(x_m, y_m), (x_M, y_M) \in A$ tali che $f(x_m, y_m) \le f(x, y) \le f(x_M, y_M)$.

In pratica, questo teorema ci aiuta nel senso che ci dice che possiamo analizzare la curva che costituisce la frontiera dell’insieme sotto esame e aggiungere ai candidati i punti di massimo e di minimo di tale curva.

Bisogna però prestare attenzione al fatto che il teorema non parla dell’esistenza dei punti nei quali la funzione ammette i valori massimo e minimo, ma soltanto dei valori stessi; ne segue che una funzione potrebbe ammettere anche infiniti punti nei quali assume i valori di massimo e minimo.

Quando utilizzo il suddetto teorema, devo specificare che lo sto utilizzando.

7.2 Vincoli di uguaglianza

Lo scopo è cercare i punti di massimo e minimo di una funzione $f(x, y)$ sotto un vincolo della forma $F(x, y) = 0$ con $F(x, y) = f(x, y) - k$, cioè $f$ ma vincolata all’insiem di livello $k$.

$x_0$ viene detto punto di massimo relativo per $f$ vicolato a $Z$ se $\exists \delta \gt 0 : f(\underline x_0) \ge f(\underline x) \forall x \in B_\delta(\underline x_0) \cap Z$.

$x_0$ viene detto punto di massimo assoluto per $f$ vincolato a $Z$ se $f(\underline x_0) \forall \underline x \in Z$.

Per i minimi, le definizioni sono analoghe.

Se $x_0$ è detto punto di estremo vincolato se è massimo o minimo vincolato.

Per trovare massimi e minimi di una funzione vincolata, esistono principalmente tre metodi: il metodo di sostituzione in coordinate cartesiane, il metodo di sostituzione in coordinate polari e il metodo dei moltiplicatori di Lagrange.

Il metodo di sostituzione in coordinate cartesiane consiste nel trovare, partendo dalla $F$, la $y$ espressa in funzione della $x$ (o viceversa) e sostituire la variabile trovata nella $f$ sotto analisi in modo da trasformare il tutto in uno studio di funzione 1-dimensionale: dopo aver trovato i massimi e i minimi della $f$ 1-dimensionale, si sostituiscono i valori trovati al posto della variabile in funzione della quale viene descritta la vriabile precedentemente utilizzata e così sono state trovate tutte le coordinate dei punti di massimo e minimo. Ad esempio, se dalla $F$ ricavo che $y = y(x)$, scrivo che $g(x) = f(x, y) = f(x, y(x))$ e studio i massimi e i minimi di $g$. Supponendo che $g$ risulti avere un massimo in $x_M$ e un minimo in $x_m$ allora le coordinate di massimo e minimo di $f(x, y)$ saranno $(x_M, y(x_M))$ e $(x_m, y(x_m))$.

Nel caso in cui l’insieme $Z = \{(x, y) : f(x, y) = 0\}$ sia una circonferenza, è possibile utilizzare il metodo di sostituzione in coordinate cartesiane che consiste nell’applicare la sostituzione

$$\begin{cases} x = r_0 \cos \theta \\ y = r_0 \sin \theta \end{cases}$$

ottenendo $g(\theta) = f(r_0 \cos \theta, r_0 \sin \theta)$ e nel studiare la funzione così ottenuta per $\theta \in [0, 2 \pi)$.

Il metodo dei moltiplicatori di Lagrange è l’equivalente del teorema di Fermat ma per i punti di estremo sul vincolo di uguaglianza.

Siano $D \sube \mathbb{R}^2$ aperto, $f,F \in \mathcal{C}^1{\mathbb{D}}$. Se $\underline x_0$ è punto di estremo vincolato a $Z$ per $f$ con $Z = \{(x, y) \in D : F(x, y) = 0\}$ e inoltre $\nabla F(x, y) \ne 0$ (leggasi “la curva è regolare”) allora esiste un $\lambda_0 \in \mathbb{R}$ detto moltiplicatore di Lagrange tale che $\lambda f(\underline x_0) = \lambda_0 \nabla F(\underline x_0)$.

In pratica, si deve risolvere il seguente sistema nonlineare a tre incognite $(x_0, y_0, \lambda_0)$

$$\begin{cases} \frac{\partial f}{\partial x} (\underline x_0) = \lambda_0 \frac{\partial F}{\partial x} (\underline x_0) \\ \frac{\partial f}{\partial y} (\underline x_0) = \lambda_0 \frac{\partial F}{\partial y} (\underline x_0) \\ F(\underline x_0) = 0 \end{cases}$$

e poi classificare le varie combinazioni soluzioni ottenute (ignorando le $\lambda$) per capire di che tipo di punti si tratta.

Siano $A \sube \mathbb{R}^2$ aperto, $f,F \in \mathcal{C}^1(A)$. Si definisce Lagrangiana la funzione di tre variabili $\mathscr{L}(x, y, \lambda) = f(x, y) - \lambda F(x, y)$ il cui gradiente posto uguale a zero risolve il sistema dei moltiplicatori di Lagrange.

Capitolo Otto: Integrali doppi

$D \sube \mathbb{R}^2$ è detta regione y-semplice se è della forma

$$D = \{(x, y) \in \mathbb{R}^2 : x \in [a, b], g_1(x) \le y \le g_2(x)\}$$

con $[a, b]$ limitato, $g_1 \le g_2$ e $g_1, g_2$ continue in $[a, b]$.

$D \sube \mathbb{R}^2$ è detta regione x_semplice se è della forma

$$D = \{(x, y) \in \mathbb{R}^2 : y \in [c, d], h_1(y) \le x \le h_2(y)\}$$

con $[c, d]$ limitato, $h_1 \le h_2$ e $h_1, h_2$ continue in $[c, d]$.

Se $D \sube R^2$ è regione semplice e $f : D \to \mathbb{R}$ è continua su $D$ allora $f$ è integrabile su $D$.

Se $D$ è unione di regioni semplici, si può integrare separatamente su ciascuna regione e poi sommare i risultati.

Se $D$ è y-semplice allora

$$\int \int_D f(x, y) dxdy = \int_a^b \left( \int_{g_1(x)}^{g_2(x)} f(x, y) dy \right) dx$$

Se $D$ è x-semplice allora

$${\int\int}_D f(x, y) dxdy = \int_c^d \left( \int_{h_1(y)}^{h_2(y)} f(x, y) dx \right) dy$$

Se $f(x, y) = f_1(x) \cdot f_2(y)$ e le due funzioni $g_1, g_2$ o $h_1, h_2$ sono costanti, il conto si può semplificare rendendolo prodotto di integrali:

$${\int\int}_D f(x, y) dxdy = \int_a^b \left( \int_{g_1(x)}^{g_2(x)} f(x, y) dy \right) dx = \int_c^d f_2(y) dy \cdot \int_a^b f_1(x) dx$$

8.1 Cambio di variabili (coordinate polari)

Se applico alla $f$ da integrare una mappa del tipo $\varphi(x, y) = \begin{pmatrix} r \cos \theta \\ r \sin \theta \end{pmatrix}$ allora ottengo che $f(\varphi(x, y)) = f(r, \theta)$ e che $f' = f'(\varphi(x, y)) \cdot \varphi'(x, y)$. Necessito di trovare $\varphi'$, per farlo utilizzo la matrice jacobiana:

$$J_\varphi(r, \theta) = \begin{bmatrix} \left[ \nabla \varphi_1(r, \theta) \right]^T \\ \left[ \nabla \varphi_2(r, \theta) \right]^T \\ \end{bmatrix} = \begin{bmatrix} \frac{\partial \varphi_1}{\partial r} & \frac{\partial \varphi_1}{\partial \theta} \\ \frac{\partial \varphi_2}{\partial r} & \frac{\partial \varphi_2}{\partial \theta} \\ \end{bmatrix} = \begin{bmatrix} \cos \theta & -r \sin \theta \\ \sin \theta & r \cos \theta \\ \end{bmatrix}$$

da cui segue che

$$|\det J_\varphi(r, \theta)| = r$$

Dunque $\varphi'(r, \theta) = r$.

Per effettuare un cambio di variabili con una mappa generica, $\varphi$ deve essere di classe $\mathcal{C}^1$, biunivoca e $\det J_\varphi(u, v) \ne 0$ e limitato $\forall u,v$.

Capitolo Nove: Integrali tripli

$E \sube \mathbb{R}^3$ è detta regione z-semplice se è della forma

$$E = \{ (x, y, z) \in \mathbb{R}^3 : (x, y) \in D, h_1(x, y) \le z \le h_2(x, y) \}$$

con $D$ regione semplice, $h_1 \le h_2$ e $h_1,h_2$ continue in $D$.

9.1 Integrazione per fili

Sia $E$ regione z-semplice, $f : E \to R$ continua in $E$, allora $f$ è integrabile su $E$ e vale la formula di integrazione per fili.

L’integrazione per fili consiste nell’integrare su di un filo (integrale singolo) e poi integrare il risultato su di un’area (integrale doppio):

$${\int\int\int}_E f(x, y, z) dxdydz = {\int\int}_D \left( \int_{h_1(x, y)}^{h_2(x, y)} f(x, y, z) dz \right) dxdy$$

Se fosse richiesto di integrare su una regione x-semplice o y-semplice allora si sotituisce la z con, rispettivamente, x e y.

9.2 Integrazione per strati.

Sia $E$ regione z-semplice, $f : E \to R$ continua in $E$, allora $f$ è integrabile su $E$ e vale la formula di integrazione per strati.

L’integrazione per strati consiste nell’integrare su di uno strato (integrale doppio) e poi integrare il risultato su un filo generico (integrale singolo):

$${\int\int\int}_E f(x, y, z) dxdydz = \int_a^b \left( {\int\int}_D f(x, y, z) dxdy \right) dz$$

dove i parametri $a$ e $b$ sono i limiti entro i quali è compresa $z$.

Per scegliere tra integrazione per fili o per strati, è necessario capire “di che forma” è il dominio e vedere se è più facile trgliarlo a fette (integrale per strati) o in fili. Tendenzialmente, se i limiti entro i quali è compresa $z$ sono costanti, è preferibile l’integrazione per strati.

9.3 Cambio di variabili (coordinate sferiche)

Il ragionamento è identico a quello del cambiamento di coordinate in coordinate polari ma cambia il determinante jacobiano.

La mappa che descrive il cambiamento di coordinate è

$$\begin{cases} T_1(r, \varphi, \theta) = r \sin \varphi \cos \theta \\ T_2(r, \varphi, \theta) = r \sin \varphi \sin \theta \\ T_3(r, \varphi, \theta) = r \cos \varphi \end{cases}$$

Dunque, per calcolare il determinante jacobiano si procede come segue:

$$J_T(r, \varphi, \theta) = \begin{bmatrix} \left[ \nabla T_1(r, \varphi, \theta) \right]^T \\ \left[ \nabla T_2(r, \varphi, \theta) \right]^T \\ \left[ \nabla T_3(r, \varphi, \theta) \right]^T \\ \end{bmatrix} = \begin{bmatrix} \frac{\partial T_1}{\partial r} & \frac{\partial T_1}{\partial \varphi} & \frac{\partial T_1}{\partial \theta} \\ \frac{\partial T_2}{\partial r} & \frac{\partial T_2}{\partial \varphi} & \frac{\partial T_2}{\partial \theta} \\ \frac{\partial T_3}{\partial r} & \frac{\partial T_3}{\partial \varphi} & \frac{\partial T_3}{\partial \theta} \\ \end{bmatrix} = \begin{bmatrix} \sin \varphi \cos \theta & r \cos \varphi \cos \theta & -r \sin \varphi \sin \theta \\ \sin \varphi \sin \theta & r \cos \varphi \sin \theta & r \sin \varphi \cos \theta \\ \cos \varphi & -r \sin \varphi & 0 \end{bmatrix} \\ \begin{align*} \det J_T(r, \varphi, \theta) &= \cos \varphi \det \begin{bmatrix} r \cos \varphi \cos \theta & -r \sin \varphi \sin \theta \\ r \cos \varphi \sin \theta & r \sin \varphi \cos \theta \\ \end{bmatrix} + r \sin \varphi \det \begin{bmatrix} \sin \varphi \cos \theta & -r \sin \varphi \sin \theta \\ \sin \varphi \sin \theta & r \sin \varphi \cos \theta \\ \end{bmatrix} \\ &= cos \varphi (r^2 \sin \varphi \cos \varphi \cos^2 \theta + r^2 \sin \varphi \cos \varphi \sin^2 \theta) + r \sin \varphi (r \sin^2 \varphi \cos^2 \theta + r \sin^2 \varphi \sin ^2 \theta) \\ &= r^2 \sin \varphi \cos^2 \varphi \cos^2 \theta + r^2 \sin \varphi \cos^2 \varphi \sin^2 \theta + r^2 \sin^3 \varphi \cos^2 \theta + r^2 \sin^3 \varphi \sin^2 \theta \\ &= r^2 \sin \varphi \cos^2 \varphi (\cos^2 \theta + \sin^2 \theta) + r^2 \sin^3 \varphi (\cos^2 \theta + \sin^2 \theta) \\ &= r^2 \sin \varphi \cos^2 \varphi + r^2 \sin^3 \varphi \\ &= r^2 \sin \varphi (\cos^2 \varphi + \sin^2 \varphi) \\ &= r^2 \sin \varphi \end{align*}$$

9.4 Massa e baricentro

Sia $E \sube \mathbb{R}^3$ regione semplice che rappresenta un corpo rigido e $\rho(x, y, z) : E \to \mathbb{R}^+$ la funzione che rappresenta la densità di massa nel punto $(x, y, z)$, allora

$$\text{Massa}(E) = {\int\int\int}_E \rho(x, y, z) dxdydz$$

Il baricentro è il punto che può essere considerato come punto di applicazione delle forze agenti sul campo. Il baricentro $(\overline x_B, \overline y_B, \overline z_B)$ si calcola nel seguente modo:

$$\overline x_B = \frac{1}{\text{Massa}(E)} \cdot {\int\int\int}_E x \cdot \rho(x, y, z) dxdydz \\ \overline y_B = \frac{1}{\text{Massa}(E)} \cdot {\int\int\int}_E y \cdot \rho(x, y, z) dxdydz \\ \overline z_B = \frac{1}{\text{Massa}(E)} \cdot {\int\int\int}_E z \cdot \rho(x, y, z) dxdydz \\$$

9.5 Cambio di variabili (coordinate cilindriche)

Il passaggio a coordinate cilindriche si applica quando $E$ è z-semplice della forma $E = \{(x, y, z) \in \mathbb{R}^3 : (x, y) \in D, h_1(x, y) \le x \le h_2(x, y)\}$ e $D$ è a simmetria radiale.

In tal caso, si procede prima integrando per fili e poi procedendo al cambio di variabili in coordinate polari:

$$j(x, y) = \int_{h_1(x, y)}^{h_2(x, y)} f(x, y, z) dz \\ {\int\int\int}_E f(x, y, z) dxdydz = {\int\int}_D j(x, y) dxdy = \int\int j(r \cos \theta, r \sin \theta) r drd\theta$$

Capitolo Dieci: Studio qualitativo EDO

Sia $A \sube \mathbb{R}^2$, $f : A \to \mathbb{R}$ continua in $A$. Se in un intorno del punto $(t_0, y_0) \in A$, $\frac{\partial f}{\partial y}(t, y)$ esiste ed è continua allora il problema di Cauchy

$$\begin{cases} y'(t) = f(t, y(t)) \\ y(t_0) = y_0 \end{cases}$$

ammette un’unica soluzione localmente in un intorno del punto $(t_0, y_0)$.

In pratica, se $f : A \sube \mathbb{R}^2 \to \mathbb{R}$ non contiene termini del tipo $(y - \overline y)^\alpha$ con $\alpha \in (0, 1)$ o $|y - \overline y|^\alpha$ con $\alpha \in (0, 1]$ allora $\frac{\partial f}{\partial y}$ esiste ed è continua in tutto $A$ e quindi tutti i problemi di Cauchy con $(t_0, y_0) \in A$ ammettono soluzione unica e quindi i grafici di soluzioni distinte non si intersecano.

Se invece $f$ contiene termini del tipo $(y - \overline y)^\alpha$ con $\alpha \in (0, 1)$ o $|y - \overline y|^\alpha$ con $\alpha \in (0, 1]$ allora $\frac{\partial f}{\partial y}$ potrebbe non esistere o non essere continua nella retta $y = \overline y$. Fuori dalla retta continua a valere l’unicità locale.

Nel caso in cui esistano due soluzioni allo stesso problema di Cauchy, queste si intersecano sempre (almeno nel punto in cui si impine il passaggio della funzione).

Nel caso in cui valga il teorema di esistenza e unicità locale in tutti i punti del dominio di $f$ e $t \in [a, b]$ è un intervallo fissato indipendente da $y$ (quindi è una striscia verticale), se $A = [a, b] \times \mathbb{R}$ è limitato, $f : A \to \mathbb{R}$ è continua e $\frac{\partial f}{\partial y}$, allora

1. se esistono due costanti $M,N \lt 0$ tali che $\forall (t, y) \in A$ vale che $|f(t, y)| \le M|y| + N$ oppure $\left| \frac{\partial f}{\partial y} (t, y) \right| \le M$ allora $\forall (t_0, y_0) \in A$ il problema di Cauchy $y(t_0) = y_0$ ha un’unica soluzione definita $\forall t \in [a, b]$
2. se per una soluzione particolare $\overline y$ esiste $k \gt 0$ tale che $\overline y(t) \le k \quad \forall t$ nel dominio di definizione di $\overline y$ allora $\overline y$ è definita $\forall t \in [a, b]$.

10.1 Studio qualitativo di EDO del primo ordine

Lo studio qualitativo di una EDO consiste nel tracciare un gragfco approssimativo della sua soluzione anche senza saperla risolvere.

Una EDO è detta autonoma se la sua $f$ non dipende da $t$, quindi se è della forma $y'(t) = f(y(t))$.

Le EDO autonome sono un sottoinsieme delle edo a variabili separabili e possono essere risolte come tali

$$y'(t) = f(y(t)) \iff \int_{t_0}^t \frac{y'(t_0)}{f(y(t))} dt = \int_{y(t_0)}^{y(t)} \frac{dy}{f(y)} = \int_{t_0}^t 1 dt$$

Se però $\frac{1}{f(y)}$ non è facilmente integrabile, è comunque possibile tracciare un grafico approssimato delle sue soluzioni attraverso lo studio qualitativo.

Se $y(t)$ è soluzione, allora anche $z(t) = y(t + c)$ lo è, infatti se $y$ è soluzione, allora $y'(t) = f(y(t))$ e quindi $z'(t) = y'(t + c) = f(y(t + c)) = f(z)$. Questa proprietà di cide che qualsiasi sia la soluzione trovata, una soluzione con la stessa forma ma translata orizzontalmente è comunque soluzione dell’equazione sotto esame.

Dato che si tratta di EDO lineari, vale il teorema di esistenza e unicità globale per il problema di Cauchy quindi in ogni punto passa una e una sola soluzione e in tutti i punti passa una e una sola soluzione, quindi le soluzioni non si intersecano.

Per disegnare una soluzione approssimativa, bisogna ricavare la linea delle fasi:

1. si disegna $f(y)$ sul piano con $y$ sull’asse delle ascisse e $f(y)$ sull’asse delle ordinate;
2. si posiziona un’asse monodimensionale (la linea delle fasi) sotto il grafico del punto 1;
3. si segna un punto sulla linea delle fasi (punto di equilibrio) in corrispondenza degli zeri della $f(y)$, ottenendo così degli intervalli;
4. si segna un afreccia verso sinistra (negativa) dove la $f(y)$ è negativa e una verso destra (positiva) dove la $f(y)$ è positiva;
5. si ruota la linea delle fasi di 90° in senso antiorario, in modo da avere le y positive in alto;
6. si disegna un piano con $t$ sull’asse delle ascisse e $y(t)$ sull’asse delle ordinate e lo si posiziona di fianco alla linea delle fasi appena ruotata;
7. sul nuovo grafico, si disegna una soluzione costante in corrispondenza di ciascun punto d’equilibrio;
8. per ogni freccia positiva sulla linea delle fasi, si disegna una funzione più o meno simile ad un sigmoide che per $t \to -\infty$ è asintotica alla soluzione costante che delimita inferiormente l’intervallo in cui ci si trova e per $t \to +\infty$ è asintotica alla soluzione costante che delimita superiormente l’intervallo in cui ci si trova;
9. per ogni freccia negativa, il ragionamento è analogo a quello per le frecce positive ma con le soluzioni costanti opposte.

Se un intervallo non è delimitato da un punto di equilibrio, allora la soluzione approssimativa tenderà a $\pm \infty$ compatibilmente con la posizione della soluzione all’interno della linea delle fasi.

E’ importante ricordare ancora una volta che, per il teorema di esistenza e unicità, nessuna soluzione si interseca con altre soluzioni, dunque le soluzioni non costanti, pur avvicinandosi sempre più a quelle costanti, non le toccheranno mai.

Se viene richiesto di disegnare una soluzione approssimativa che passa in un punto particolare, si transla orizzontalmente la soluzione approssimativa trovata nell’intervallo che contiene il punto finchè la soluzione non passa per tale punto.

10.2 Sistemi differenziali autonomi nel piano

Un sistema differenziale autonomo è un sistema differenziale della forma

$$\underline y'(t) = \underline f(\underline y(t))\begin{cases} f_1(y_1(t), y_2(t)) \\ f_2(y_1(t), y_2(t)) \end{cases}$$

con $f : A \sube \mathbb{R}^3$ continua che non dipende esplicitamente da $t$.

Se per le equazioni si ha la linea delle fasi, per i sistemi 2-dimensionali si ha il piano delle fasi.

Sono detti punti di equilibrio i punti nei quali $f(y_1, y_2) = \underline 0$ e corrispondono con le soluzioni costanti dell’equazone.

Una traiettoria/orbita è invece, una curva che rappresenta una famiglia di soluzioni della forma $\underline y(t + c)$ (i punti di equilibrio sono inclusi in questa definizione).

Per disegnare le soluzioni approssimative, si deve disegnare il piano delle fasi:

1. si ricava la matrice $A$ del sistema, così come gli autovalori e gli autovettori;
2. per ciascun autovettore, si sisegna una retta passante per l’origine e diretta come l’autovettore;
3. per ciascuna retta, se l’autovalore associato all’autovettore da cui è originata è positivo, allora si disegnano due frecce (una da un alto dell’origine e l’altra dall’altro) in direzione uscente, se l’autovettore è negativo allora la direzione è entrante;
4. si combinano le informazioni come in foto

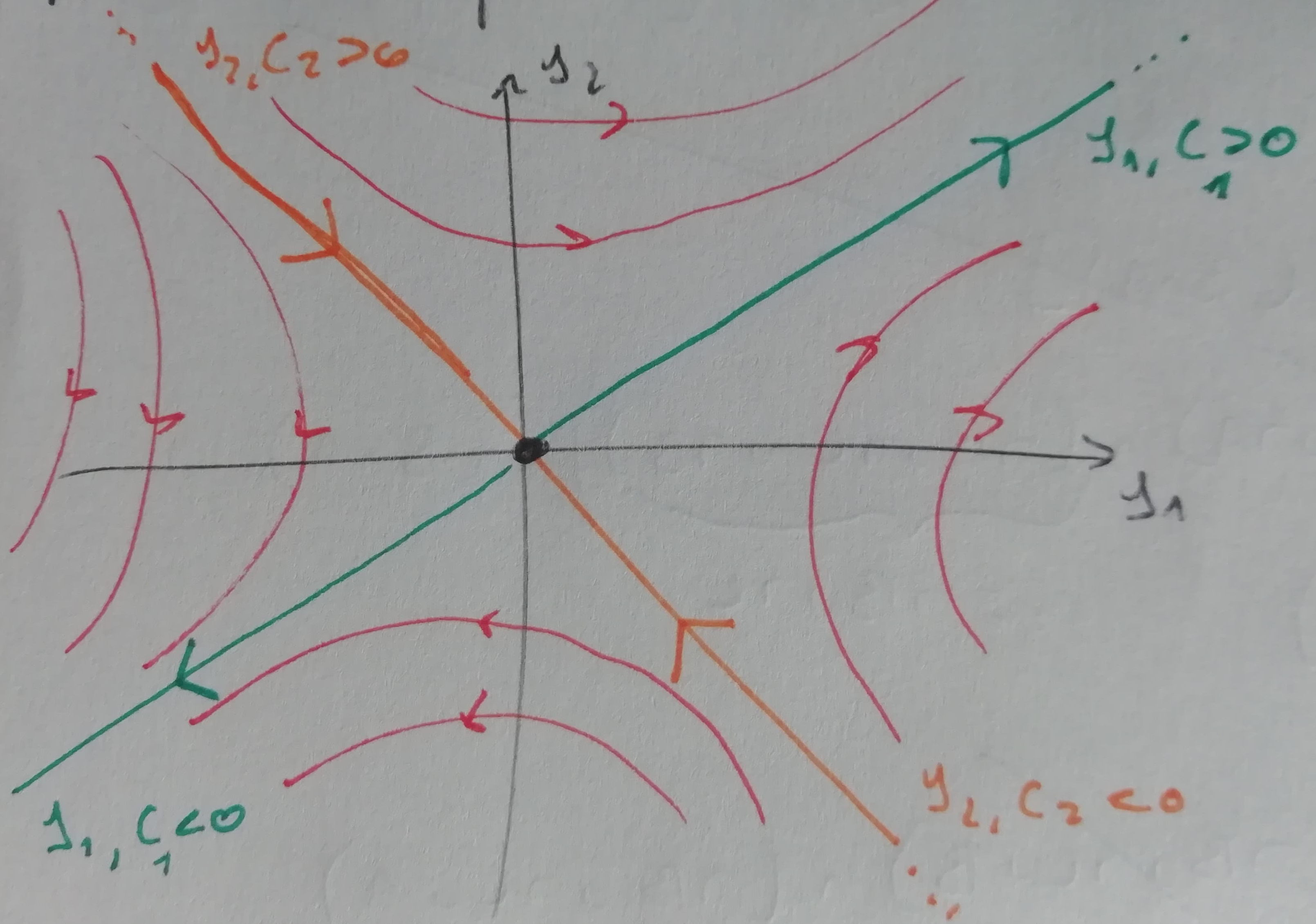
In caso di autovalori diversi con lo stesso segno, le famiglie di soluzioni sono tangenti alla retta con autovalore più piccolo in modulo.

Sia nell’asse che nel piano delle fasi, se una soluzione costante ha soltanto frecce entranti, è detta punto di equilibrio stabile, se invece ha anche una sola freccia uscente, è detta di equilibrio instabile.

Capitolo Finale: Varie ed eventuali

Di seguito lista delle dimostrazioni da conoscere per l’esame:

1. Formula risolutiva EDO del primo ordine lineari
2. Teorema di struttura dell’integrale generale di EDO del secondo ordine lineari omogenee
3. Calcolo del raggio di convergenza
4. Calcolo dei coefficienti di Fourier
5. Invarianza della lunghezza di una curva per riparametrizzazione
6. Differenziabilità implica continuità
7. Formula del gradiente
8. Ortogonalità del gradiente alle curve di livello
9. Criterio della matrice hessiana
10. Cambio di variabili in coordinate sferiche

Di seguito tabella riassuntiva dei vari insiemi di convergenza delle serie di funzioni

Insieme	Convergenza	Significato
$J$		Insieme di definizione delle $f_n(x)$
$E \sube J$	Semplice/puntuale	Insieme di punti nel quale la serie di funzioni converge
$I \sube J$	Totale	Intervallo nel quale ogni termine della serie di funzioni può essere maggiorata in modulo da una serie numerica convergente