Onde Elettromagnetiche e Mezzi Trasmissivi — Appunti TiTilda

Indice

Capitolo Uno: Segnali

Un segnale s(t) è una grandezza fisica che varia nel tempo e nello spazio. Per trasmettere informazioni, un segnale non deve essere periodico.

s(t) = \begin{cases} v(t) & \to \text{ tensione} & \left[V\right]\\ i(t) & \to \text{ corrente} & \left[A\right]\\ \vec{e}(t) & \to \text{ campo elettrico} & \left[\frac{V}{m}\right]\\ \vec{h}(t) & \to \text{ campo magnetico} & \left[\frac{A}{m}\right]\\ \end{cases}

I segnali digitali sono sequenze di valori discreti nel tempo che prendono il nome di simboli.

1.1 Perdite di trasmissione

1.2 Serie di Fourier

Ogni segnale periodico può essere scomposto in una sommatoria di sinusoidi con coefficienti complessi:

s(t) = \sum_{k=-\infty}^{+\infty} S_k e^{j2\pi k f_0t}

dove f_0 è la frequenza fondamentale e S_k sono i coefficienti complessi:

S_k = \left|S_k\right| e^{j\phi_k}

Formule di Eulero

\begin{cases} \cos(2\pi f_0 t) = \displaystyle\frac{e^{j2\pi f_0 t} + e^{-j2\pi f_0 t}}{2}\\ \sin(2\pi f_0 t) = \displaystyle\frac{e^{j2\pi f_0 t} - e^{-j2\pi f_0 t}}{2j}\\ \end{cases}

ovvero:

S_1 S_{-1}
\cos \displaystyle\frac{1}{2} \displaystyle\frac{1}{2}
\sin \displaystyle\frac{1}{2j} -\displaystyle\frac{1}{2j}

1.3 Trasformata di Fourier

La trasformata di Fourier è una generalizzazione della serie di Fourier per segnali non periodici.

S(f) = \int_{-\infty}^{+\infty} s(t) e^{-j2\pi ft}\, dt

È possibile ottenere il segnale originale a partire dalla trasformata di Fourier:

s(t) = \int_{-\infty}^{+\infty} S(f) e^{j2\pi ft}\, df

Traslazione nel tempo

\begin{align*} s(t) &\to S(f)\\ s(t-\tau) &\to S(f) e^{-j2\pi f \tau}\\ \end{align*}

Traslare nel tempo un segnale ne modifica la fase, ma non la sua banda:

\begin{align*} Z(f) &= S(f) e^{-j2\pi f \tau}\\ &\updownarrow\\ \measuredangle Z(f) &= \measuredangle S(f) - 2\pi f \tau\\ \end{align*}

Traslazione in frequenza

\begin{align*} s(t) &\to S(f)\\ s(t) e^{j2\pi f_0 t} &\to S(f-f_0)\\ \end{align*}

La banda del nuovo segnale ha la stessa ampiezza di quella originale, ma è centrata in una nuova frequenza portante incrementata di f_0.

1.4 Risposta in frequenza di un mezzo di trasmissione

La risposta in frequenza di un mezzo di trasmissione H(f) è la sua capacità di trasmettere segnali con frequenze diverse.

S_{out}(f) = S_{in}(f) \cdot H(f)

Il modulo di H(f) descrive l’attenuazione del segnale, mentre la fase descrive la distorsione.

\begin{align*} \left|H(f)\right| &= \left| \frac{S_{out}(f)}{S_{in}(f)} \right|\\ \measuredangle H(f) &= \measuredangle S_{out}(f) - \measuredangle S_{in}(f)\\ \end{align*}

Affinché esista H(f), il mezzo di trasmissione deve essere lineare e tempo-invariante (in questo corso, tutti i mezzi di trasmissione sono lineari e tempo-invarianti).

In questo corso, tutti i mezzi di trasmissione sono passivi (il modulo di H(f) è sempre minore di 1).

1.5 Rappresentazione in scala logaritmica

Decibel (base 10)

\begin{align*} X &\to X_{\text{dB}} = 10 \log_{10} X\\ X_{\text{dB}} &\to X = 10^{\frac{X_{\text{dB}}}{10}}\\ \end{align*}

Neper (base e)

\begin{align*} X &\to X_{\text{Np}} = \ln X\\ X_{\text{Np}} &\to X = e^{X_{\text{Np}}}\\ \end{align*}

Per passare da una base all’altra, basta moltiplicare per il fattore di conversione:

\begin{align*} X_{\text{dB}} &= 10 \log_{10} X = 10 \frac{\ln X}{\ln 10} = 10 \frac{X_{\text{Np}}}{\ln 10}\\ X_{\text{Np}} &= \ln X = \ln 10 \frac{X_{\text{dB}}}{10} = \ln 10 \frac{X_{\text{dB}}}{10}\\ \end{align*}

Potenza

Per la potenza, si usa la scala logaritmica in base 10 con unità di misura \text{dBm} (decibel-milliwatt):

P\ [\text{dBm}] = 10 \log_{10} \frac{P\ [\text{mW}]}{1\ \text{mW}}

esempio: \begin{align*}P &= \mu\text{W} = 10^{-6} \text{ W} = 10^{-3} \text{ mW}\\ P_{\text{dBm}} &= 10 \log_{10} \frac{10^{-3}}{1} = -30\ \text{dBm}\\ \end{align*}

Capitolo Due: Linee di trasmissione

Una linea di trasmissione è un mezzo di trasmissione che permette di trasmettere segnali elettrici da un punto a un altro.

Data la lunghezza l del mezzo di trasmissione e la lunghezza d’onda \lambda del segnale:

2.1 Modello a parametri distribuiti

Il modello a parametri distribuiti è un modello a circuito equivalente che considera la linea di trasmissione come una serie di tratti infinitesimi dz, più piccoli della lunghezza d’onda del segnale.

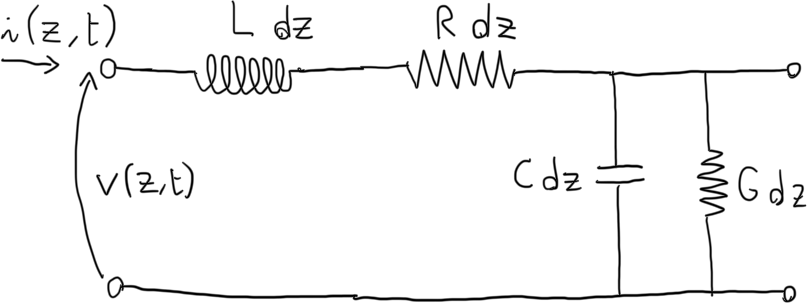
Modello a parametri distribuiti

Sono presenti:

2.2 Equazioni dei telegrafisti

Applicando le leggi di Kirchhoff, si ottengono le due equazioni differenziali che prendono il nome di Equazioni dei Telegrafisti (nel dominio del tempo):

\begin{cases} \displaystyle - \frac{\partial v(z,t)}{\partial z} = R \frac{\partial i(z,t)}{\partial z} + L \frac{\partial i(z,t)}{\partial t}\\ \\ \displaystyle - \frac{\partial i(z,t)}{\partial z} = G \frac{\partial v(z,t)}{\partial z} + C \frac{\partial v(z,t)}{\partial t}\\ \end{cases}

Nel dominio dei fasori, le equazioni dei telegrafisti diventano:

\begin{cases} \displaystyle - \frac{d V(z)}{d z} = (R + j \omega L)\, I(z)\, e^{j \omega t}\\ \\ \displaystyle - \frac{d I(z)}{d z} = (G + j \omega C)\, V(z)\, e^{j \omega t}\\ \end{cases}

2.3 Equazioni delle onde

Derivando nuovamente ciascuna equazione rispetto a z e sostituendo l’altra equazione, si ottengono le equazioni delle onde per le tensioni e le correnti:

\begin{cases} \displaystyle - \frac{d^2 V(z)}{d z^2} = (R + j\omega L) (G + j\omega C)\, V(z) = 0\\ \\ \displaystyle - \frac{d^2 I(z)}{d z^2} = (R + j\omega L) (G + j\omega C)\, I(z) = 0\\ \end{cases}

Costante di propagazione

Definita la costante di propagazione (complessa) \gamma come:

\gamma = \sqrt{(R + j\omega L) (G + j\omega C)}

le equazioni delle onde diventano:

\begin{cases} \displaystyle \frac{d^2 V(z)}{d z^2} - \gamma^2 V(z) = 0\\ \\ \displaystyle \frac{d^2 I(z)}{d z^2} - \gamma^2 I(z) = 0\\ \end{cases}

Nota: \gamma si misura in \left[m^{-1}\right].

\gamma = \Re\{\gamma\} + j \Im\{\gamma\} = \alpha + j\beta

dove \alpha è la costante di attenuazione (misurata in \left[\frac{Np}{m}\right]) e \beta è la costante di fase (misurata in \left[\frac{rad}{m}\right]).

Lunghezza d’onda

La lunghezza d’onda \lambda (misuata in metri) è il periodo spaziale di una sinusoide che si propaga nello spazio allo scorrere del tempo:

\lambda = \frac{v_f}{f_0}\ \left[\text{m}\right]

dove v_f è la velocità di fase e f_0 è la frequenza fondamentale. Poiché v_f dipende dal mezzo di trasmissione, anche \lambda dipende dal mezzo di trasmissione.

Nello spazio vuoto, la velocità di fase è pari alla velocità della luce c = 3 \cdot 10^8\ \left[\frac{m}{s}\right].

La lungheza d’onda è sempre legata alla costante di fase \beta:

\lambda = \frac{2\pi}{\beta}

Nelle linee senza perdite, la lunghezza d’onda \lambda è pari a:

\lambda = \frac{1}{f \sqrt{LC}}

Soluzione delle equazioni delle onde (per linee senza perdite, ovvero R = 0, G = 0)

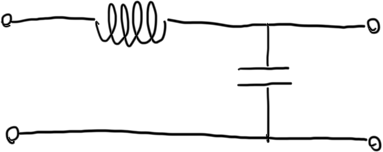
Linea senza perdite

Nel caso di un mezzo di trasmissione senza perdite (R = 0, G = 0), si ha che:

\begin{align*}\gamma^2 = &\, (j \omega L)(j \omega C) = - \omega^2 LC\\ \gamma = &\, \pm j \omega \sqrt{LC} \end{align*}

In altre parole, essendo in un caso ideale, la costante di attenuazione \alpha è nulla e la costante di fase \beta è pari a \omega \sqrt{LC} (la costante di propagazione \gamma è puramente immaginaria).

La soluzione delle equazioni delle onde è:

\begin{cases} V(z) &= &V_0^+ e^{-j \beta z} + V_0^- e^{j \beta z}\\ I(z) &= &I_0^+ e^{-j \beta z} - I_0^- e^{j \beta z}\\ \end{cases}

Nel dominio del tempo, la soluzione è:

\begin{cases} v(z,t) &= &V_0^+ \cos(\omega t - \beta z) + V_0^- \cos(\omega t + \beta z)\\ i(z,t) &= &I_0^+ \cos(\omega t - \beta z) - I_0^- \cos(\omega t + \beta z)\\ \end{cases}

Essendo la fase \beta z lineare con f, in una linea senza perdite non si ha alcuna dispersione cromatica.

2.4 Onda progressiva e regressiva

La parte V_0^+ \cos(\omega t - \beta z) rappresenta un’onda che si propaga in avanti (progressiva/propagante), mentre la parte V_0^- \cos(\omega t + \beta z) rappresenta un’onda che torna indietro (regressiva).

L’obiettivo dei problemi di adattamento è quello di eliminare le onde regressive.

Il coefficiente di riflessione sul carico \Gamma_L indica quanto dell’onda incidente viene riflessa dal carico:

\Gamma_L = \frac{V_0^-}{V_0^+}

2.5 Impedenza caratteristica

L’impedenza caratteristica Z_0 di una linea di trasmissione è l’impedenza costante (che non cambia in diversi punti della linea) associata alla linea di trasmissione che lega la tensione alla corrente nella soluzione delle equazioni delle onde. In una linea senza perdite:

Z_0 = \sqrt{\frac{L}{C}}\ \ \left[ \Omega \right]

L’impedenza caratteristica lega la corrente dell’onda progressiva e quella dell’onda regressiva alla tensione dell’onda progressiva e di quella regressiva, rispettivamente, prese singolarmente:

\begin{cases} I_0^+ &= &\displaystyle \frac{V_0^+}{Z_0}\\ I_0^- &= &\displaystyle \frac{V_0^-}{Z_0}\\ \end{cases}

L’impedenza caratteristica non dipende da:

2.6 Adattamento di impedenza

Considerando un carico Z_L collegato a una linea di trasmissione con impedenza caratteristica Z_0, si ha che:

V_0^- = \frac{Z_L - Z_0}{Z_L + Z_0} V_0^+

In altre parole, se Z_L = Z_0, non ci sono onde regressive.

2.7 Impedenza d’onda

L’impedenza d’onda Z(z) è l’impedenza vista da un punto z della linea di trasmissione. In una linea senza perdite:

Z(z) = \frac{V(z)}{I(z)} = \frac{V_0^+ e^{-j \beta z} + V_0^- e^{-j \beta z}}{\underbrace{\frac{V_0^+}{Z_0}e^{-j\beta z}}_{I_0^+} - \underbrace{\frac{V_0^-}{Z_0} e^{+j \beta z}}_{I_0^-}} = Z_0 \frac{1 + \Gamma_L e^{+2j\beta z}}{1 - \Gamma_L e^{+2j\beta z}}

Alternativamente, definita l la distanza dal carico (z :=-l), si ha che:

Z(l) = Z_0 \frac{Z_L + j Z_0 \tan(\beta l)}{Z_0 + j Z_L \tan(\beta l)}

dove \beta = \frac{2\pi}{\lambda}

Ultima modifica:
Scritto da: Alessandro Modica