Cinematica

La cinematica studia i moti degli oggetti senza preoccuparsi delle cause.

S(t) è la legge oraria che descrive la posizione di una particella in funzione del tempo. Per estrarre la traiettoria, bisogna fare in modo di rimuovere il parametro tempo dalla traiettoria.

Una posizione può anche essere descritta da un vettore:

\vec r(t) = \begin{bmatrix} x(t) \\ y(t) \\ z(t) \end{bmatrix} = x(t) \hat u_x + y(t) \hat u_y + z(t) \hat u_z

Di seguito alcune definizioni importanti.

Velocità scalare media e istantanea

v_m = \frac{\Delta S}{\Delta t} \qquad S(t) = \int_{t_0}^t v(t)dt + S(t_0)

E’ importante notare che la legge oraria non corrisponde alla distanza: assumendo S(t_0) = 0,

\Delta S = \int_{t_0}^t v(t)dt \qquad d = \int_{t_0}^t |v(t)dt|

La velocità scalare istantanea si ottiene facendo il limite per \Delta t \to 0:

v = \lim_{\Delta t \to 0} \frac{\Delta S}{\Delta t} = \frac{dS}{dt}

Velocità vettoriale media e istantanea

\vec v_m = \frac{\Delta \vec r}{\Delta t} = \frac{\Delta x}{\Delta t} \hat u_x + \frac{\Delta y}{\Delta t} \hat u_y + \frac{\Delta z}{\Delta t} \hat u_z

La velocità vettoriale istantanea si ottiene facendo il limite per \Delta t \to 0:

\vec v = \lim_{\Delta t \to 0} \frac{\Delta \vec r}{\Delta t} = \frac{d \vec r}{dt} = v_x \hat u_x + v_y \hat u_y + v_z \hat u_z

Il vettore \vec v è sempre tangente alla traiettoria, infatti:

\vec v =\lim_{\Delta t \to 0} \frac{d \vec r}{dt} = \lim_{\Delta t \to 0} \frac{\Delta \vec r}{\Delta S} \cdot \frac{\Delta S}{\Delta t} = \underbrace{\lim_{\Delta S \to 0} \frac{\Delta \vec r}{\Delta S}}_{\to 1} \cdot \underbrace{\lim_{\Delta t \to 0} \frac{\Delta S}{\Delta t}}_{= v}

Andando al limite, |d \vec r| = |dS| quindi lo spostamento (e, di conseguenza, la velocità) è sempre tangente alla traiettoria.

Accelerazione vettoriale media e istantanea

\vec a_m = \frac{\Delta \vec v}{\Delta t}

Anche qui, per l’accelerazione istantanea, si fa il limite \Delta t \to 0

\vec a = \lim_{\Delta t \to 0} \frac{\Delta \vec v}{\Delta t} = \frac{d \vec v}{dt} = \frac{d}{dt} \left( \frac{d \vec r}{dt} \right) = \frac{d^2 \vec r}{dt^2}

Tutti i moti che non sono il moto rettilineo unforme, sono accelerati.

L’accelerazione è composta da una componente tangenziale ed una normale:

\vec a = \frac{d \vec v}{dt} = \frac{d}{dt}(v \hat u_t) = \underbrace{\frac{dv}{dt} \hat u_t}_{a_t} + \underbrace{v \frac{d \hat u_t}{dt}}_{a_n}

Ora devo dimostrare che \vec a_n \perp \vec a_t, di conseguenza devo dimostrare che \hat u_n \cdot \hat u_t = 0. Calcolo la derivata di \hat u_t \cdot \hat u_t:

\frac{d(\hat u_t \cdot \hat u_t)}{dt} = \frac{d \hat u_t}{dt} \cdot \hat u_t + \hat u_t \cdot \frac{d \hat u_t}{dt} = 2 \hat u_t \cdot \frac{d \hat u_t}{dt}

Siccome \hat u_t \cdot \hat u_t = |\hat u_t|^2 = 1^2 = 1 è costante, allora la sua derivata vale zero:

2 \hat u_t \cdot \frac{d \hat u_t}{dt} = 0

da cui ricavo che \hat u_t \perp (\hat u_t)' e quindi \vec a_t \perp \vec a_n (vanno in direzione \hat u_t e (\hat u_t)')

Se \vec a_n = 0 allora ho un moto rettilineo.

Se \frac{dv}{dt} = 0 allora ho un moto uniforme (non necessariamente rettilineo).

La madre di tutti i moti

Dato un corpo con posizione iniziale, velocità iniziale e accelerazione, la sua posizione in funzione del tempo si calcola nel seguente modo:

\vec r(t) = \vec r_0 + \vec v_0t + \frac 12 \vec a t^2

Menzione particolare meritano il moto circolare e il moto armonico (pendolo, molla e simili)

Moto circolare

La posizione di una particella che compie moto circolare è la seguente:

\begin{cases} x(t) = R \cos(\theta(t)) \\ y(t) = R \sin(\theta(t)) \end{cases}

ove R indica il raggio della circonferenza e

\theta(t) = \theta_0 + \omega_0 t + \frac 12 \alpha t^2

Con \omega si indica la pulsazione o velocità angolare mentre con \alpha l’accelerazione angolare:

\omega(t) = \frac{d \theta}{dt} \qquad \alpha(t) = \frac{d \omega}{dt}

Altre formule comode per il moto circolare sono:

\vec v = \omega R \hat u_t = \vec \omega \times \vec r \qquad \vec a_r = \omega^2 R \hat u_r = \frac{v^2}{R} \hat u_r

ove \vec \omega =\omega \hat u_z ed è perpendicolare al piano su cui giace la traiettria (grazie alla regola della mano destra, conosco anche il senso di percorrenza).

Moto armonico

Il moto armonico è il moto di un oggetto che oscilla nel tempo.

x(t) = A \cos(\omega t + \theta_0) \\ v(t) = -A \omega \sin(\omega t + \theta_0) \\ a(t) = -A \omega^2 \cos(\omega t + \theta_0) = - \omega^2 x(t)

Dalla definizione di accelerazione ottengo che

\frac{d^2x}{dt^2} = -\omega^2x \implies \frac{d^2x}{dt^2} + \omega^2 x = 0

ed ho ottenuto un’equazione differenziale.

Il moto armonico è un tipo di moto periodico.

Moto periodico

Un moto è periodico se

\begin{cases} \vec r(t + nT) = \vec r(t) \\ \vec v(t + nT) =\vec v(t) \end{cases}

T è il periodo: indica ogni quanto tempo \vec r e \vec v si ripetono.

f = \frac 1T = \frac{\omega}{2 \pi} \qquad \omega = 2 \pi f

Moto piano in coordinate polari

E’ possibile esprimere uno stesso punto sia in cordinate cartesiane (x, y) che in coordinate polari (r, \theta).

\vec r = r_x \hat u_x + r_y \hat u_y \qquad \vec v = \frac{d \vec r}{dt} = \frac{d(r \hat u_r)}{dt} = \underbrace{\frac{dr}{dt} \hat u_r}_{\text{Velocità radiale}} + r \frac{d \hat u_r}{dt} = v_r \hat u_r + r \omega \hat u_\theta \qquad \frac{d \hat u_r}{dt} = \vec \omega \times \hat u_r = \omega \hat u_\theta

Dinamica

La dinamica studia le cause del moto degli oggetti.

Per comprendere la dinamica e i 3 principi che la regolano, è necessario sapere che un sistema di riferimento inerziale è tale quando ha origine in un punto che non è soggetto ad accelerazioni.

I tre principi della dinamica, in quanto principi, si possono verificare sperimentalmente in laboratorio ma non si possono dimostrare.

Per quanto precisi siano gli strumenti, siccome sulla terra siamo in un sistema di riferimento non inerziale, ci saranno sempre degli errori.

Per convenzione un sistema di riferimento inerzial eè quello che ha origine nel sole e con gli assi x, y, e z che pntano alle stelle fisse.

Tutto ciò che è relativo ad un sistema di riferimento inerziale è a sua volta un sistema di riferimento inerziale.

Di seguito alcune nozioni fondamentali per la comprensione di quanto seguirà.

Massa inerziale

Immaginiamo di prendere due masse m_1 e m_2 e di schiacciarle contro una molla: quando le si rilascia partiranno a velocità diverse.

\frac{ |\vec v_1| }{ |\vec v_2| } = \frac{ |\Delta \vec v_1| }{ |\Delta \vec v_2| } = k_{1,2} = \frac{m_2}{m_1}

k non dipende da quanto comprimiamo ma solo dalle due masse scelte.

Se scelgo m_1 come massa campione e gli assegno il valore 1, posso ripetere lo stesso esperimento anche con m_3, m_4, \dots e misurare tutte le masse.

La massa m_1 è il chilogrammo di platino-iridio conservato a Parigi.

Quantità di moto

La quantità di moto è letteralmente quanta massa si sta muovendo e a quale velocità.

\vec P = m \vec v

Siccome la massa è additiva, allora lo è anche la quantità di moto:

m = m_1 + \dots + m_n \qquad \vec P = m_1 \vec v_1 + \dots + m_n \vec v_n

Per il principio di conservazione della quantità di moto, in un sistema chiuso la quantità di moto si conserva:

\Delta \vec P = \Delta \vec P_1 + \Delta \vec P_2 = m_1 \Delta \vec v_1 + m_2 \Delta \vec v_2 = 0 \implies m_1 \Delta \vec v_1 = -m_2 \Delta \vec v_2

I 3 principi della dinamica

1 - Principio d’inerzia

Un corpo non soggetto ad interazioni permane nel suo stato di quiete o si muove di moto rettilineo uniforme.

Questo principio si chiama così perchè descrive l’inerzia di un corpo a cambiare di stato.

Questo principio è valido solo in un sistema di riferimento inerziale.

2 -

Un corpo puntiforme soggetto ad interazioni subisce un’ accelerazione.

La forza è quella che esprime le interazioni e si misura in [N] = \left[ \frac{kg \cdot m}{s^2} \right]

\vec F = \frac{d \vec P}{dt} = \frac{d(m\vec v)}{dt} = m \frac{d \vec v}{dt} = m \vec a

Anche la forza è additiva: se una particella interagisce co più particelle, la risultante delle forze F è data da

\vec F = \sum_{i = 1}^n \vec F_n

Un corpo è in quiete se (condizione necessaria e sufficiente)

\begin{cases} \vec v = 0 & \qquad \text{In un certo istante } t \\ \vec F = 0 & \qquad \forall t \end{cases}

Se \vec F = 0 allora si è in equilibrio. Ci sono 3 tipi di equilibrio:

• stabile: se muovo l’oggetto di un infinitesimo, questo ritorna nella posizione originale (pallina in una scodella)
• instabile: se muovo l’oggetto di un infinitesimo, questo comincia ad accelerare e ad andarsene (pallina su un pallone da calcio)
• indifferente: se muovo l’oggetto di un infinitesimo, questo rimane fermo nella nuova posizione (pallina su un tavolo)

3 -

Ad ogni azione corrisponde una reazione uguale e contraria.

E’ notabile il fatto che questo teorema non specifica niente sulla direzione delle forze: se avessi due porse di verso opposto su due direzioni parallele, queste rispetterebbero il terzo principio ma nella realtà non funziona così.

Questo principio deriva anch’esso dal fatto che, in un sistema isolato, la quantità di moto si conserva, infatti:

\vec P = \vec P_1 + \vec P_2 \qquad \frac{d \vec P}{dt} = 0 \iff \frac{d \vec P_1}{dt} = -\frac{d \vec P_2}{dt}

da cui si ricava che \vec F_1 = - \vec F_2

Teorema dell’impulso

\vec I = \int_{t_1}^{t_2} \vec F \, dt = \int_{t_1}^{t_2} \frac{d \vec P}{\cancel{dt}} \, \cancel{dt} = \int_{t_1}^{t_2} d \vec P =\Delta \vec P

Interazioni

Ci sono diversi tipi di interazioni che dipendono sia dalle caratteristiche dei corpi che interagiscono che dalla loro distanza.

Interazione gravitazionale

E’ responsabile dell’attrazione tra corpi dotati di massa gravitazionale (che a livello macroscopico corrisponde alla massa inerziale mentre a livello quantistico no) e ha raggio d’azione infinito.

\vec F = -\gamma \frac{m_1, m_2}{r^2} \hat u_r \qquad \gamma = 6.67 \cdot 10^{-11} \frac{N \cdot m^2}{kg^2}

ove \gamma (a volte nota anche come G) è la costante di gravitazione universale, r indica la distanza tra le due masse e \hat u_r è la direzione che va dalla prima massa alla seconda e viceversa.

Interazione elettromagnetica

E’ responsabile dell’attrazione e repulsione di oggetti carichi, è responsabile della stabilità degli atomi, delle forze di attrito, di contatto ed elettrostatiche.

Ha un raggio d’azione infinito.

\vec F = \frac{1}{4 \pi \varepsilon_0} \frac{q_1 q_2}{r^2} \hat u_r \qquad \varepsilon_0 = 8.854 \cdot 10^{12} \frac{C}{m^2N}

Interazione nucleare debole

E’ responsabile del decadimento \beta, ha un raggio d’azione dell’ordine di 10^{-18}m (per intenderci, un atomo è circa 10^{-10}m).

Interazione nucleare forte

E’ responsabile per la stabilità del nucleo ed è la più forte attualmente conosciuta (all’interno del suo raggio d’azione che è dell’ordine di 10^{-15}m).

In particolare è quella forza che mantiene assieme i quark: - quark diversi: viene mediata da scambio di pioni e attrae tra loro protoni e neutroni - quark uguali: viene mediata da scambio di gluoni e tiene interi i protoni

Forze principali e altre misure utili

Di seguito le principali forze utilizzate, alcune misure ad esse relative e moti tipici ove applicabile.

Forza peso

La forza peso è causata dall’attrazione gravitazionale.

\vec F_p = m \vec g \qquad g \simeq 9.81 \frac{m}{s^2} \text{ (sulla terra)}

Per trovare il valore di un’accelerazione di gravità generica

a = -\gamma \frac{M}{r^2}

ove M è la massa del corpo che causa l’attrazione gravitazionale e r è il suo raggio. Nel caso della terra si ha che

E’ utile sapere che la massa della Terra è M_t = 5.98 \cdot 10^24 kg e che il suo raggio è r_T = 6371 km, in questo modo si può calcolare l’accelerazione di gravità terrestre.

g = -\gamma \frac{M_T}{r_T^2} = -6.67 \frac{N \cdot m^2}{kg^2} \cdot 10^{-11} \frac{5.98 \cdot 10^{24} kg}{(6.37 \cdot 10^6)^2 m^2} \simeq 9.81 \frac{m}{s^2}

Densità

La densità è la misura di quanta massa c’è in un dato volume

\rho_m = \frac mV

Se l’oggetto è uniforme

\rho = \rho_m = \frac{dm}{dV}

e ha senso misurare il peso specifico

P_{sm} = \rho_m g = \frac{mg}{V} \qquad P_s = \rho g = \frac{dm}{dV} g

Reazione vincolare

La reazione vincolare è la forza che non fa sprofondare gli oggetti quando li si poggia su un tavolo:

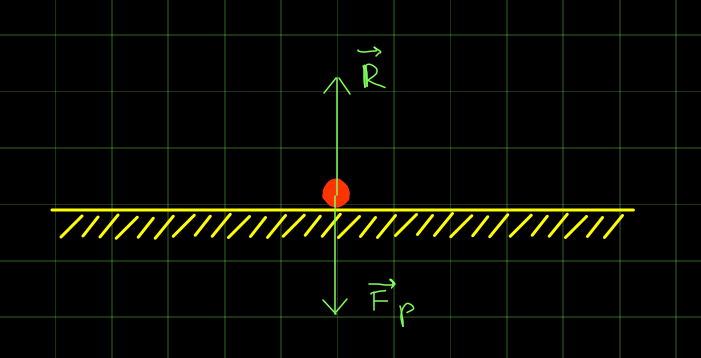
La reazione vincolare può essere composta da una parte normale al piano (\vec N) e da una parte parallela (nel caso di forze d’attrito ma saranno descritte dopo).

Se \vec R < 0 allora l’oggetto non è poggiato contro niente e si considera \vec R = 0.

Forza elastica

La forza elastica è un tipo di forza che dipende dalla posizione: se fisso un corpo ad una molla e lo sposto, questo subirà una forza proporzionale allo spostamento.

\vec F_{el} = -k \Delta l \hat u_x

ove k è la costante elastica della molla, \Delta l è lo spostamento rispetto alla condizione di eqilibrio e \hat u_x è la direzione dello spostamento parallelo alla molla.

Le costanti elastiche delle molle in serie e parallelo si comportano come i condensatori:

k_{par} = \sum_i k_i \qquad \frac{1}{k_{ser}} = \sum_i \frac{1}{k_i}

In assenza di attriti, oggetti attaccati ad una molla libera che non si trova in equilibrio, compiono moto armonico:

\frac{d^2x}{dt^2} + \underbrace{\frac{k}{m}}_{=\omega^2}x = 0 \implies x(t) = A \cos(\omega t + \varphi_0)

Per trovare A e \varphi_0, si necessita di avere a disposizione le condizioni iniziali dell’oggetto in movimento:

\begin{cases} x(0) = x_0 \\ v(0) = 0 \end{cases} \implies \begin{cases} A \cos(\varphi_0) = x_0 & \implies A = x_0 \\ -A \omega \sin (\varphi_0) = 0 & \implies \varphi_0 = 0 \end{cases}

Forza di attrito radente

E’ la componente che si oppone al moto degli oggetti su un piano scabro.

Ne esistono di due categorie: statico e dinamico.

La forza di attrito statico è subita da un oggetto che senza attrito si muoverebbe ma, siccome c’è l’attrito, sta fermo.

La forza di attrito dinamico è subita da un oggetto in movimento ed è costante.

Entrambe le forze non dipendono dalla massa degli oggetti ne dall’area di contatto ma soltanto dal vincolo normale (è dovuto alle forze di attrazione elettrostatiche).

F_{as} \le \mu_s |\vec N| \qquad F_{ad} = \mu_d |\vec N| \qquad \mu_s > \mu_d

Entrambe hanno direzione opposta al moto (o al moto che ci sarebbe se non ci fossero).

Se il piano è liscio, \mu_s = \mu_d = 0.

Forza di Lorentz

La forza di Lorentz è la forza subita dalle particelle cariche (di carica q) che si trovano in un campo elettrico o magnetico: - Se il campo è un campo magnetico e \vec B è il vettore di induzione magnetica, \vec F_{\mathscr L} = q(\vec v \times \vec B) - Se il campo è un campo elettrico ed \vec E è il vettore campo elettrico, \vec F_{\mathscr L} = q \vec E.

Si può dimostrare che particelle soggette soltanto a forza di Lorentz si muovono percorrendo traiettoria circolare.

Lavoro ed energia

Se una forza \vec F sposta una massa di una distanza d\vec r allora

\delta \mathscr L = \vec F \cdot d \vec r \implies \mathscr L ^\gamma_{AB} = {\int_A^B}_\gamma \delta \mathscr L = {\int_A^B}_\gamma \vec F \cdot d \vec r

ove \gamma è la traiettoria e A e B sono i punti di partenza e arrivo.

Siccome la forza è additiva, allora anche il lavoro lo è. Il lavoro può essere scomposto in componenti x, y e z. In generale il lavoro dipende dalla traiettoria \gamma (se non è vero allora si parla di forze non conservative).

Teorema delle forze vive / Teorema dell’energia cinetica

\mathscr L_{AB} = \int_A^B \delta \mathscr L = \int_A^B \vec F \cdot d \vec r = \int_A^B dE_k = E_k(B) - E_k(A) = \Delta E_k

Questo teorema è sempre valido solo in sistemi di riferimento inerziali. E’ valido anche in sistemi di riferimento non inerziali se si tiene conto delle forze apparenti.

Segue dimostrazione.

Sappiamo che \mathscr L = {\int_A^B}_\gamma \delta \mathscr L, \vec F = m \vec a, \vec a = \frac{d \vec v}{dt} e che d \vec r = \vec v \, dt e vogliamo dimostrare che \delta \mathscr L = \Delta E_k.

Per la dimostrazione è anche necessario sapere che

\frac{d}{dt} \left( \vec v \cdot \vec v \right) = 2\vec v \cdot \frac{d \vec v}{dt} \implies \vec v \cdot d \vec v = \frac 12 d(\vec v \cdot \vec v) = \frac 12 d \vec v^2

\delta \mathscr L = \vec F \cdot d \vec r = m \vec a \cdot d \vec r = m \frac{d \vec v}{dt} \cdot \vec v \, dt = m \, d \vec v \cdot \vec v = \frac 12 m \, d \vec v^2 = dE_k

Di conseguenza

\mathscr L = \int \delta L = \int dE_k = \Delta E_k ## Forze conservative

Per comprendere le forze conservative, è necessario conoscere il significato di gradiente e rotore.

Gradiente

Il gradiente indica la direzione di massima crescita di una funzione (verrà utilizzato principalmente per le forze).

Sia f(x, y, z) una funzione scalare, allora

\text{grad}(f) = \vec \nabla f = \frac{\partial f}{\partial x} \hat u_x + \frac{\partial f}{\partial y} \hat u_y + \frac{\partial f}{\partial z} \hat u_x

è la direzione di massima crescita della funzione.

Rotore

\text{rot} f = \det \begin{bmatrix} \hat u_x & \hat u_y & \hat u_z \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ F_x & F_y & F_z \end{bmatrix}

Definizioni di forza conservativa

Ci sono 5 definizioni equivalenti di forza conservativa, 4 che si basano su proprietà globali e 1 che si basa su proprietà locali.

Una forza è conservativa se:

1. \mathscr L = {\int_A^B}_\gamma \vec F \cdot d \vec r non dipende da \gamma
2. \exists E_p(\vec r) scalare tale per cui \mathscr L_{AB} = E_p(A) - E_p(B) = - \Delta E_p
3. \oint_\gamma \delta \mathscr L = E_p(A) - E_p(A) = 0 \quad \forall \gamma \text{ chiusa}
4. \vec F = - \vec \nabla E_p(\vec r)
5. \text{rot}(F) = 0

Forze centrali a simmetria sferica

Una forza è centrale a simmetria sferica se è esprimibile nella forma

\vec F = - \gamma \frac{m_1 m_2}{r^2} \hat u_r

Le forze centrali a simmetria sferica sono conservative, segue dimostrazione.

\begin{align*} \mathscr L &= \int_A^B \delta \mathscr L \\ &= \int_A^B \vec F \cdot d \vec r \\ &= \int_A^B F(\vec r) \cdot d \vec v \\ &= \int_{r_A}^{r_B} -\gamma \frac{m_1 m_2}{r^2} \,dr \\ &= \gamma m_1 m_2 \int_{r_A}^{r^B} -\frac{1}{r^2} \, dr \\ &= \gamma m_1 m_2 \left( \frac{1}{r_B} - \frac{1}{r_A} \right) \\ &= -\gamma \frac{m_1 m_2}{r_A} + \gamma \frac{m_2 m_2}{r_B} \\ &= E_p(A) - E_p(B) \end{align*}

ove E_p(r) = \gamma \frac{m_1 m_2}{r} + c e c = 0 \implies E_p(r \to \infty) \to 0.

Esempi di forze non conservative

La forza di attrito radente non è conservativa: se si parla di attrito statico, non c’è movimento e pertanto il lavoro si annulla mentre se si parla di attrito dinamico allora

\mathscr L_{AB}^\gamma = {\int_A^B}_\gamma \vec F \cdot d \vec r = {\int_A^B}_\gamma -\mu_d |\vec N| \hat u_v \cdot d \vec r

Siccome \vec v = \frac{d \vec r}{dt} allora la roba sopra si puo scrivere anche come

-\mu_d |\vec N| {\int_A^B}_\gamma \hat u_v \cdot v \, dt = -\mu_d |\vec N| {\int_A^B}_\gamma |\vec r| \ne 0

Neanche la forza di attrito viscoso è conservativa: se F_{av} = -\beta \vec v allora

\mathscr L_{AB}^\gamma = {\int_A^B}_\gamma \vec F_{av} \cdot d \vec r = {\int_A^B}_\gamma -\beta \vec v \cdot \vec v \, dt = -\beta {\int_A^B}_\gamma |\vec v|^2 \, dt \le 0

Energia meccanica

L’energia meccanica di un oggetto è la somma della sua energia cinetica con la sua energia potenziale (ne esistono di vari tipi).

Siccome la forza è additiva, lo è anche l’energia meccanica

E_m = E_p + E_k \qquad E_m = \sum_i {E_m}_i

Se tutte le forze sono conservative d(E_k + E_p) = 0, altrimenti d(E_k + E_p) = \mathscr L_ad.

\underbrace{\delta \mathscr L_{tot}}_{dE_k} = \delta \mathscr L^{(NC)} + \underbrace{\delta \mathscr L^{(C)}}_{-dE_p} \implies dE = dE_k + dE_p = \delta \mathscr L^{(NC)} \implies \Delta E = \mathscr L^{(NC)}

Con il termine trasformismo dell’energia si intende il fatto che l’energia potenziale può trsformarsi in energia cinetica e viceversa purchè la somma non cambi.

Formule per calcolare le varie energie

• Energia cinetica: E_k = \frac 12 m v^2
• Energia potenziale gravitazionale: E_{pg} = mgh oppure U = -\gamma \frac{m_1 m_2}{r}
• Energia potenziale elastica: E_{pe} = \frac 12 k (\Delta l)^2

Potenza

La potenza è la quantità di energia trasferita nell’unità di tempo.

P = \frac{\delta \mathscr L}{dt} \\ \delta \mathscr L = P \, dt \implies \mathscr L = \int_{t_1}^{t_2} P \, dt \implies P = \frac{\vec F \cdot d \vec r}{dt} = \vec F \cdot \vec v

Si misura in Watt: W = \frac J S.

Dinamica relativa

La dinamica classica si occupa di studiare le interazioni tra oggetti in un sistema di riferimento inserziale fisso. Con la dinamica relativa, si possono studiare anche i moti relativi a sistemi di riferimento che accelerano: in questo caso andranno studiate anche le cosiddette forze apparenti.

Sia S un sistema di riferimonto inerziale e S' un sistema di riferimento che si muove e ruota rispetto ad S, allora S' è un sistema di riferimento non inerziale.

\vec r = \vec r' + \vec R \\ \vec v = \frac{d \vec r}{dt} = \frac{d \vec r'}{dt} + \frac{d \vec R}{dt} = \vec v' + \omega \times \vec r' + \vec v_{o'} = \vec v' + \vec v_T \\ \vec a = \frac{d \vec v}{dt} = \frac{d \vec v'}{dt} + \frac{d \omega}{dt} \times \vec r' + \vec \omega \times \frac{d \vec r'}{dt} + \frac{d \vec v_{o'}}{dt} = \vec a' + \underbrace{2(\vec \omega \times \vec v)}_{= \vec a_c, \text{ accelerazione di Coriolis}} + \underbrace{\overbrace{\frac{d \vec \omega}{dt} \times \vec r'}^{\vec \alpha \times \vec r'} + \vec \omega \times (\vec \omega \times \vec r)}_{=a_T, \text{ accelerazione di trascinamento}} + \vec a_{o'}

Dinamica in sistemi di riferimento non inerziali

Se \vec F = m \vec a allora \vec F' = m \vec a' quindi \vec F = m \vec a = \underbrace{m \vec a'}_{\vec F'} + m \vec a_{co} + m \vec a_T

Some si può notare, le due forze non corrispondono: vengono introdotte delle forze fittizie per compensare il fatto che il sistema di riferimento non è inerziale.

\vec F_{co} = -m \vec a_{co} \qquad \vec F_T = -m \vec a_T

Non è possibile riutilizzare il principio d’inerzia:

v = 0, F = 0 \implies \vec F' = \vec F + \vec F_{co} + \vec F_T

Gravitazione

Per comprendere la gravitazione, è necessario aver compreso le nozioni di momento di un vettore/forza/quantità di moto.

Momento di tutte le robe quì sopra

Il momento del vettore \vec F rispetto al polo O è definito come \vec \tau_{(O)} = \vec r \times \vec F da cui si può dedurre che |\vec \tau_{(O)}| = |\vec r ||\vec F| \sin \theta = |\vec F| r \sin \theta e non dipende dal vettore \vec r scelto, infatti, supponendo \vec r' = \vec r + \vec a allora

\vec \tau_{(O)} = \vec r' \times \vec F = (\vec r + \vec a) \times \vec F = \vec r \times \vec F + \vec a \times \vec F = \vec r \times \vec F

Il momento di una forza è esattamente la stessa cosa ma con \vec F rappresentante una forza.

Il momento di una quantità di moto invece è \vec L_{(O)} = \vec r \times \vec P = \vec r \times m \vec v ed è sempre perpendicolare a posizione e velocità.

\frac{d \vec L_{(O)}}{dt} = \frac{d}{dt}(\vec r \times m \vec v) = \frac{d \vec r}{dt} \times m \vec v + \vec r \times m \frac{d \vec v}{dt} = \vec v \times m \vec v + \vec r \times m \vec a = 0 + \vec r \times \vec F = \vec \tau_{(O)}

da cui

\frac{d \vec L_{(O)}}{dt} = \vec \tau_{(O)}

Se il polo O non è costante e si muove con velocità \vec v_O'?

\vec L_{(O')}= \vec r' \times m \vec v \qquad \vec \tau_{(O')} = \frac{d \vec L_{(O')}}{dt} + \vec v_O' \times m \vec v

In caso di moto circolare uniforme, v = \omega r quindi

\vec L_{(O)} = RmR \omega \hat u_z = mR^2 \vec \omega

In caso di forze assiali, \vec L_{(O)} è costante per cui \vec \tau_{(O)} = 0 ma ciò non vuol dire che \sum F = 0.

Gravitazione - Leggi di Kepler

1. Le orbite dei pianeti sono ellittiche e il sole sta in uno dei due fuochi
2. Il vettore posizione copre aree uguali in tempi uguali (quindi, la velocità areolare si conserva)
3. Il quadrato del periodo di rotazione è proporzionale al cubo del semiasse maggiore

Energia potenziale gravitazionale

Come già accennato nella sezione sull’energia, esiste un’enrgia potenziale gravitazionale dipendente solamente dalla distanza:

E_p(r) = -\gamma \frac{m_1 m_2}{r} + c

ove E_p(r \to \infty) = 0 \implies c = 0

Se ho un’orbita circolare (consentita dalla prima legge) allora

a = a_c \implies ma_c = \frac{mv^2}{r} = \frac{\gamma m_1 m_2}{r^2} \\ E = E_k + E_p = \frac 12 \gamma \frac{m_1 m_2}{r} - \gamma \frac{m_1 m_2}{r} = - \frac 12 \gamma \frac{m_1 m_2}{r} \le 0 \text{ sempre}

Ma E_k(r \to \infty) < 0 non ha senso quindi non posso avere orbite che vanno all’infinito:

• E = min(E): orbita circolare
• E < 0: orbita chiusa
• E = 0: orbita parabolica
• E > 0: orbita iperbolica

Velocità di fuga

La velocità di fuga è quella velocità che va conferita ad un oggetto per permettergli di arrivare ad n altezza prestabilita.

L’idea è quella di aumentare abbastanza l’energia meccanica dell’oggetto fornendogli velocità per permetterlgi di sollevarsi e di arrivare all’infinito con energia pari a zero:

E(\infty) = \frac 12 m_1 v^2 - \gamma \frac{m_1 m_2}{r} = 0 \implies v = 0

Visto che l’energia si conserva allora

E_i = E_f \implies \frac12 m_1 v_{fuga}^2 - \gamma \frac{m_1 m_2}{r_{iniziale}} = 0

da cui si può ricavare la velocità di fuga

v_{fuga} = \sqrt{\frac{2gm_2}{r}}

In un orbita ellitica, \vec L_{(O)} è costante: |\vec L_{(O)}| = mr_pv_p = |\vec L_{(O)}| = mr_av_a, ove il pedice _a indica i valori relativi all’afelio/apogeo (il punto dell’orbita più lontano dal sole) mentre il pedice _p indica i valori relativi al perielio/perigeo (il punto dell’orbita più vicino al sole) e m indica la massa del pianeta.

Campo gravitazionale

Sia \vec F la forza di gravità e \mathscr {\vec G} = \frac{\vec F}{m} l’accelerazione (che non dipenda dalla massa che subisce la forza ma soltanto dalla massa che la esercita).

U viene detto potenziale gravitazionale:

U = \frac{E_p(r)}{m} = \frac{-\gamma \frac{Mm}{r}}{m} = -\gamma \frac{M}{r}

Allora

\vec F = -\vec \nabla E_p \qquad \mathscr{\vec G} = - \vec \nabla U

Ora si rennde necessario comprendere il concetto di flusso di un vettore per poi poter utilizzare il teorema di Gauss.

Flusso di un vettore

Il flusso di un vettore può essere inteso come la quantità di vettore che passa attraverso una superficie in una data quantità di tempo.

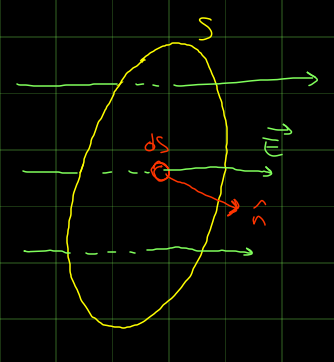
Il flusso del vettore E che passa attraverso un infinitesimo della superficie S è

d \varphi = \vec E \cdot d \vec S = \vec E \cdot \hat n \, dS = E \,dS\cos \theta

dunque il flusso di \vec E che passa per l’intera superficie S è

\varphi_S(\vec E) = \int_S d \varphi = \int_S \vec E \cdot d \vec S = \int_S \vec E \cdot \hat n \, dS

Teorema di Gauss

Normalmente, computare un calcolo del genere è estremamente difficile con una superficie generica ma non con una sfera. Il flusso di potenziale gravitazionale \varphi_S (\mathscr{\vec G}) attraverso una sfera di raggio r e centrata sulla massa puntiforme M è:

\varphi_S(\mathscr{\vec G}) = \int_S -\frac{\gamma M}{r^2} \hat u_r \cdot d \vec S = \int_S -\frac{\gamma M}{r^2} (\hat u_r \cdot \hat u_r) \,dS = -\gamma \frac{M}{r^2} \int_S dS = -\gamma \frac{M}{r^2} 4 \pi r^2 = -\gamma 4 \pi M

Se piazzo un’altra massa all’esterno della spera, entra tanto flusso quanto non esce e quindi il conto non cambia.

Riassumendo,

\varphi_S (\mathscr{\vec G}) = -4\pi M_{interna} = -4 \pi \gamma \int_S \rho(\vec r) \cdot d \vec r

ed ho così ottenuto il teorema di Gauss.

Moto nel campo gravitazionale

Ovviamente valido per tutte le forze centrali a simmetria sferica.

Abbiamo moto piano, E_m = E_k + {E_p}_g = \frac 12 m v^2 + E_p(r).

\vec v = \vec v_r + \vec v_\theta = \frac{dr}{dt} \hat u_r + r \frac{d \theta}{dt} \hat u_\theta \implies |\vec v|^2 = \left( \frac{dr}{dt} \right)^2 + r^2 \frac{L_{(O)}^2}{m^2r^4}

utilizzando il fatto che

L_{(O)} = mr^2 \vec \omega = m r \frac{d \theta}{dt} \hat u_\theta \implies \frac{d \theta}{dt} = \frac{L_{(O)}}{mr^2}

quindi

E_m = \frac 12 m \left( \frac{dr}{dt} \right)^2 + \frac 12 m r^2 \frac{L_{(0)}^2}{m^2r^4} + E_p(r) = \frac 12 m \left( \frac{dr}{dt} \right) ^2 + \underbrace{\frac 12 \frac{L_{(0)}^2}{mr^2} + E_p(r)}_{\text{Energia potenziale efficace}}

ed ho trasformato il problema in uno monodimensionale.

Ora calcolo l’accelerazione:

\vec a = \frac{d \vec v}{dt} = \frac{d}{dt} \left( \frac{dr}{dt} \hat u_r + r \frac{d \theta}{dt} \hat u_\theta \right) = \underbrace{\frac{d^2 r}{dt^2}\hat u_r}_{\text{radiale}} + \frac{dr}{dt} \vec \omega \times \hat u_r + \frac{dr}{dt}\frac{d \theta}{dt} \hat u_\theta + r \frac{d^2 \theta}{dt^2} \hat u_\theta + \underbrace{r \frac{d \theta}{dt} \vec \omega \times \hat u_\theta}_{\text{radiale}}

Siccome ci interessa solo la distanza dal centro, considero solo l’accelerazione radiale:

\vec a_r = \frac{d^r}{d t^2} \hat u_r - r \left( \frac{d \theta}{dt} \right)^2 \hat u_r = \left( \frac{d^2r}{dt^2} - \frac{L_{(0)}^2}{m^2 r^4}r \right)

Ora, siccome F(r) = ma_r allora

m\frac{d^2r}{dt^2} - m\frac{L_{(0)}^2}{m^2 r^3} = F(r) \implies m \frac{d^2r}{dt^2} = F(r) + \underbrace{\frac{L_{(0)}^2}{mr^3}}_{\text{forza centrifuga fittizia}} = F_{eff}(r)

quindi

E = \frac 12 m \left( \frac{dr}{dt} \right)^2 + E_p(r) + \frac{L_{(0)}^2}{2mr^2} = \frac 12 m \left( \frac{dr}{dt} \right)^2 + \left[ \underbrace{-\gamma \frac{Mm}{r}}_{(1)} \underbrace{\frac{L_{(0)}^2}{2mr^2}}_{(2)} \right]

Similmente a quanto detto in questo paragrafo la E_m, è possibile determinare la forma dell’orbita:

• E_m < \min(E_m): impossibile
• E_m = \min(E_m): orbita circolare
• \min(E_m) < E_m < 0: orbita ellittica
• E_m = 0: orbita iperbolica
• E_m > 0: orbita parabolica